Maximum area of a strange triangle
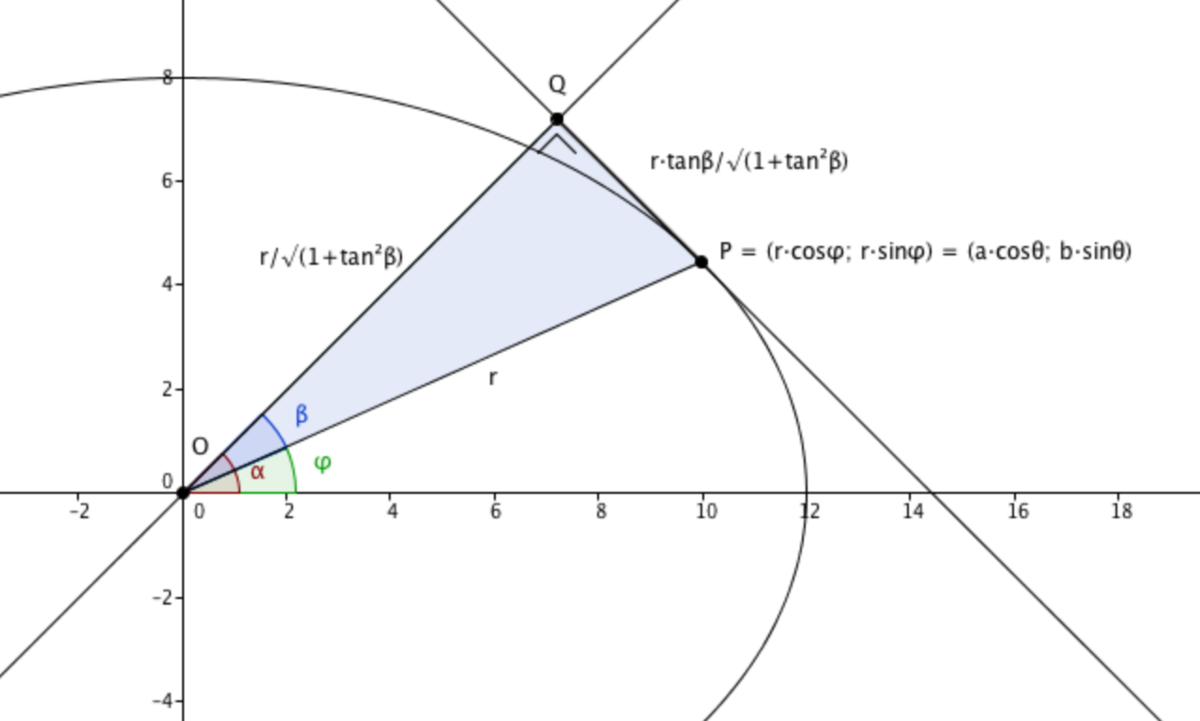
Consider an ellipse 1 4 4 x 2 + 6 4 y 2 = 1 . A line is drawn tangent to the ellipse at a point P . A line segment drawn from the origin to a point Q on this line is perpendicular to this tangent line.
Find the maximum area of △ P O Q .
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
great one!!!
Interesting fact: O Q will always have slope 1 , and P will always be the point where its tangent has slope − 1 .
a 2 x 2 + b 2 y 2 = 1 ⟺ b 2 x 2 + a 2 y 2 = a 2 b 2
Let P = ( a cos θ ; b sin θ ) , so that in polar coordinates, P = ( r cos ϕ ; r sin ϕ ) with r 2 = a 2 cos 2 θ + b 2 sin 2 θ and tan ϕ = a cos θ b sin θ , so that r 2 = 1 + tan 2 θ 1 + b 2 tan 2 θ and tan ϕ = a b tan θ
Slope of tangent is given by y ′ . b 2 x 2 + a 2 y 2 = a 2 b 2 ⟹ ( b 2 x 2 + a 2 y 2 ) ′ = ( a 2 b 2 ) ′ ⇔ 2 b 2 x + 2 a 2 y ⋅ y ′ = 0 ⇔ y ′ = a 2 y − b 2 x .
Slope of perpendicular O Q is y ′ − 1 = b 2 x a 2 y = b 2 a cos θ a 2 b sin θ , but this slope is tan α : tan α = b a tan θ , and so we have: tan θ = a b tan α , tan ϕ = a 2 b 2 tan α and r 2 = a 2 + b 2 tan 2 α a 4 + b 4 tan 2 α
Now, tan β = tan α − ϕ = 1 + tan α tan ϕ tan α − tan ϕ : tan β = a 2 + b 2 tan 2 α ( a 2 − b 2 ) tan α
O Q = 1 + tan 2 β r and P Q = 1 + tan 2 β r tan β , so searched area is A = 2 1 O Q ⋅ P Q = 2 1 ⋅ 1 + tan 2 β r 2 tan β = 2 1 ⋅ ( a 2 + b 2 tan 2 α ) 2 + ( a 2 − b 2 ) 2 tan 2 α r 2 ( a 2 − b 2 ) tan α ( a 2 + b 2 tan 2 α ) = 2 1 ⋅ ( a 4 + b 4 tan 2 α ) ( 1 + tan 2 α ) r 2 ( a 2 − b 2 ) tan α ( a 2 + b 2 tan 2 α ) = 2 1 ⋅ 1 + tan 2 α ( a 2 − b 2 ) tan α
A = 2 a 2 − b 2 ⋅ sin α cos α A is maximal when α = 4 π A m a x = 4 a 2 − b 2
Let tangent to any point P ( a c o s θ , b s i n θ ) on the ellipse a 2 x 2 + b 2 y 2 = 1 be drawn.
Equation of tangent is a x c o s θ + b y s i n θ = 1
O Q = ∣ a 2 c o s 2 θ + b 2 s i n 2 θ 1 ∣
Note that P Q is the distance of center to normal at P
Equation of normal is c o s θ a x − s i n θ b y = a 2 − b 2
P Q = ∣ c o s 2 θ a 2 + s i n 2 θ b 2 a 2 − b 2 ∣
Δ P O Q = 2 1 ( O Q ) ( P Q )
Δ P O Q = 2 ( a 2 t a n θ + b 2 c o t θ ) a b ( a 2 − b 2 )
It is easy to maximize this expression.
Δ P O Q m a x = 4 a 2 − b 2
Substitute the values to get Δ P O Q m a x = 2 0