Maximum current in circuit!
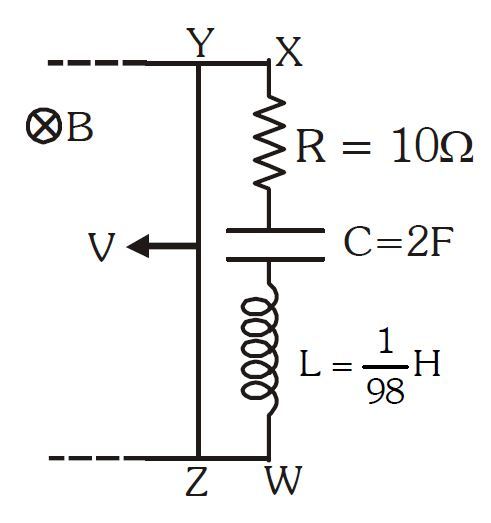 In the figure shown magnetic field
is constant and uniform and in the direction perpendicular to the plane of paper. Velocity of a conducting wire
is varying with time as
. Find the value of
(in
) so that heat generated in circuit will be maximum (neglect friction and resistance of rails).
In the figure shown magnetic field
is constant and uniform and in the direction perpendicular to the plane of paper. Velocity of a conducting wire
is varying with time as
. Find the value of
(in
) so that heat generated in circuit will be maximum (neglect friction and resistance of rails).
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
P R = I 2 R
I is maximum at Resonance.
So ω = L C 1 = 7 r a d / s