Maximum extension?

Classical Mechanics Level 5

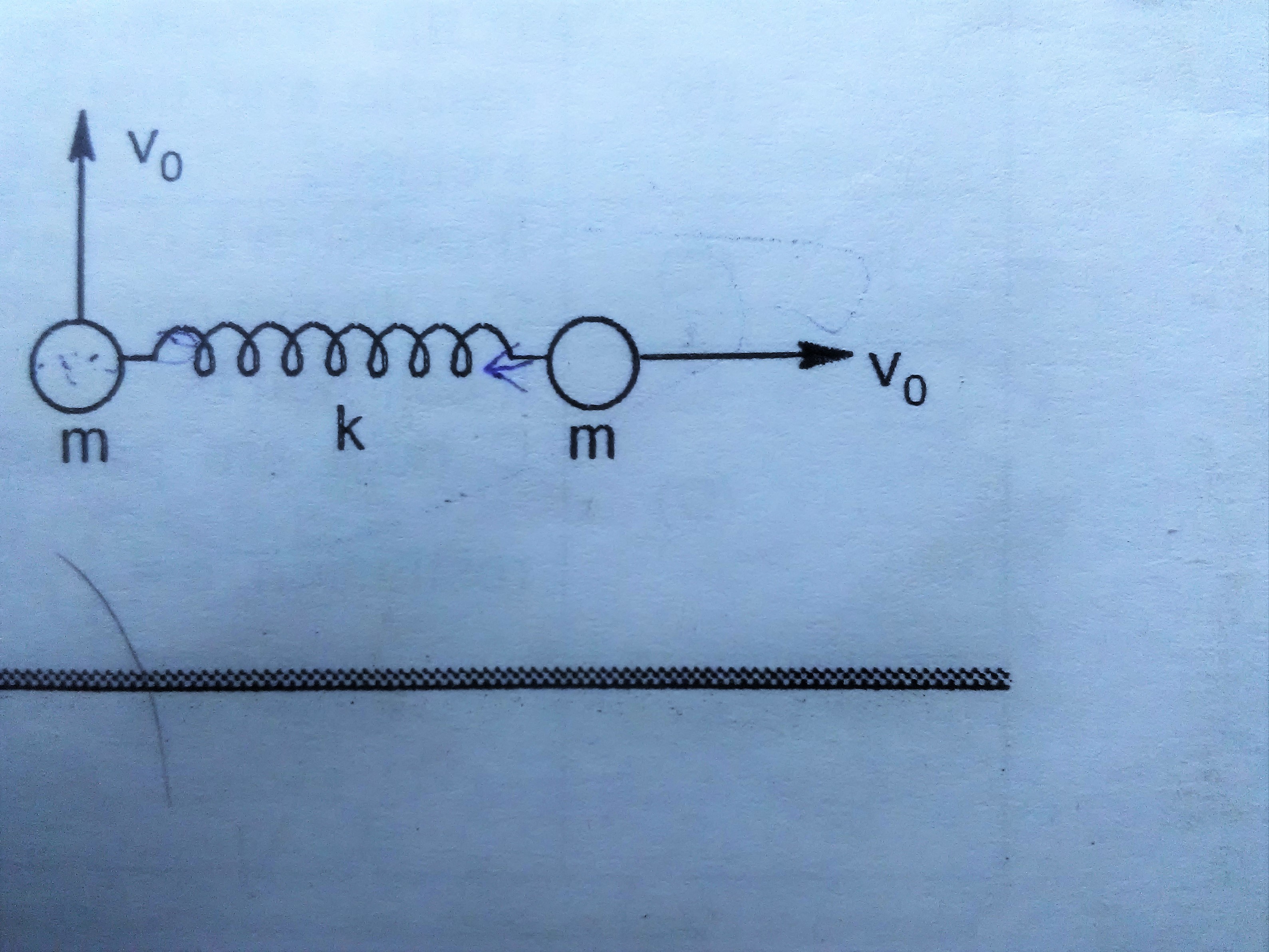
Two small spheres of mass 1 kg 1\text{ kg} each are connected to each other by means of an unstretched spring of force constant k = 100 N/m k=100\text{ N/m} and natural length 2.4 m 2.4\text{ m} .

The system is placed on a smooth horizontal surface and the two spheres are given velocity v v as shown in the figure below. The maximum elongation in spring is found to be 0.4 m 0.4\text{ m} during subsequent motion.

Calculate v v in m/s \text{m/s} . Take 31 = 5.6 \sqrt{31} = 5.6 .

-


The answer is 5.

Anshul Shrivastava by ANSHUL SHRIVASTAVA , 21, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Archit Tripathi
Dec 22, 2016

Let the maximum elongation in the spring be x x .

Conserving the angular momentum about C.M, we get

v l 2 = ( l + x ) u v\frac{l}{2} = (l + x)u

given, x = 0.4 x = 0.4

l = 2.4 l = 2.4

u u = speed of the sphere in C.M frame at maximum elongation

By applying conservation of energy, we get

2 m v 2 2 = 1 2 ( 2 m ) ( 2 v 2 ) 2 + 2 m u 2 2 + k x 2 2 2 \frac{mv^{2}}{2} = \frac{1}{2}(2m)(\frac{\sqrt{2}v}{2})^{2} + 2\frac{mu^{2}}{2} + \frac{kx^{2}}{2} .

Solving this equation we get v = 5 m / s v = \boxed{5}m/s .

5 Helpful 0 Interesting 0 Brilliant 0 Confused

Should nt it be ( l/2 + x) instead of ( l+x)

Aniswar S K - 4 years, 2 months ago
Abhisek Mohanty
Mar 10, 2017

Actually i have a doubt......if possible #spandan please have a look......Actually i tried to study the motion from the body whose mass is m and has been given a vertical velocity.So with respect to this body the other body has one horizontal and other downward velocity of same magnitude.So now its velocity is = root(2) * v. Now i applied conservation of mechanical energy. But got different answer. Could any one clarify the mistake, i mean where i did wrong. ??????

1 Helpful 0 Interesting 0 Brilliant 0 Confused

Vertical.???...Oh you followed the conventional way...No problem you can do that way as well.But make use of the fact that when there is maximum extension the velocity of the other body must be perpendicular to the spring.....And forgot tagging??☺☺

Spandan Senapati - 4 years, 3 months ago

Log in to reply

@Spandan Senapati Do we also have to include work done by pseudo forces in that case?

Kushagra Sahni - 3 years, 6 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...