Maximum of magnitude

Nice solutions, everyone! Here's another solution: $|z|=\left|z+\frac1z-\frac1z\right|\le \left|z+\frac1z\right|+\left|\frac1z\right|=2+\frac1{|z|}.$ The rest should be trivial. I liked this solution because there was no bash. ^_^

We have $\begin{aligned} (z+z^{-1})({\overline z} + {\overline z}^{-1}) &= 4 \\ |z|^2 + |z|^{-2} + {\overline z} z^{-1} + z{\overline z}^{-1} &= 4 \end{aligned}$ Let $w = {\overline z} z^{-1}.$ Then $|w|=1$ and the equation becomes $\begin{aligned} |z|^2 + |z|^{-2} + 2 \text{ Re}(w) &= 4 \\ |z|^2 + |z|^{-2} &= 4 - 2 \text{ Re}(w). \end{aligned}$ We want to maximize the left side of this equation, as it is an increasing function of $|z|$ for $|z|>1.$ Since $\text{Re}(w)$ is between $-1$ and $1,$ the right side is at most $6.$ So the maximum occurs when it is $6,$ which is when $w = -1,$ or ${\overline z} = -z,$ or $z = ri$ for some real number $r.$ In that case, we get $\begin{aligned} |z|^2 + |z|^{-2} &= 6 \\ |z|^4 - 6|z|^2 + 1 &= 0 \\ \end{aligned}$ and solving via the quadratic equation gives $|z|^2 = 3 \pm 2\sqrt{2}.$ The plus sign gives a larger $|z|,$ and the positive square root of $3+2\sqrt{2}$ is $1 + \sqrt{2},$ so the answer is $\fbox{2.414}.$

Put $z=x+iy$ and rewrite the given expression as $\left|z^2+1 \right| = 2|z|$ . Squaring both sides and rearranging, $\begin{aligned} \left(x^2-y^2+1 \right)^2+4x^2 y^2 &= 4\left( x^2+y^2 \right) \\ \left( x^2-y^2 \right)^2+2\left( x^2-y^2 \right)+1+4x^2 y^2 &= 4\left( x^2+y^2 \right) \\ \left( x^2+y^2 \right)^2+2\left( x^2-y^2 \right)+1 &= 4\left( x^2+y^2 \right) \\ \left( x^2+y^2 \right)^2-2\left( x^2+y^2 \right)+1 &= 4y^2 \\ \left( x^2+y^2-1 \right)^2 &= (2y)^2 \\ \left( x^2+y^2-1-2y \right) \left( x^2+y^2-1+2y \right)&=0 \end{aligned}$

where the last line comes from rewriting as a difference of two squares. Completing the square in each factor,

$\red{\left( x^2+(y-1)^2-2 \right)} \blue{\left( x^2+(y+1)^2-2 \right)}=0$

For the product to be zero, (at least) one of the factors has to be zero. Equating the red factor to zero gives a circle centred at $(0,1)$ with radius $\sqrt2$ ; equating the blue factor to zero gives a circle centred at $(0,-1)$ with radius $\sqrt2$ . So the locus of points satisfying the original condition is just two intersecting circles, as below:

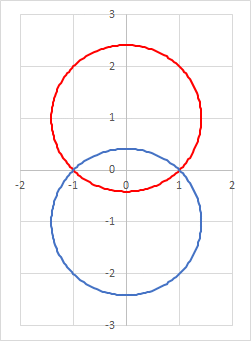
It's clear from the geometry that $|z|$ is maximised when $z=\left( 1+\sqrt2 \right)i$ , ie $|z|=\boxed{1+\sqrt2}$ .

---

One final point: it seems there may be a shortcut to this solution, without rewriting $z$ in terms of reals, if we note that $|z^2+1|=|z-i|\cdot |z+i|$ . I haven't managed to find one, though - any ideas?

Let $z=x+iy$ . Then $|z+\dfrac{1}{z}|=2\implies x^4+2x^2y^2+y^4-2x^2-6y^2+1=0\implies 4x^3dx+4xy^2dx+4x^2ydy+4y^3dy-4xdx-12ydy=0$ . $|z|=\sqrt {x^2+y^2}=$ maximum $\implies 2xdx+2ydy=0\implies dy=-\dfrac{x}{y}dx\implies 4x^3dx+4xy^2dx-4x^3dx-4xy^2dx-4xdx+12xdx=0\implies x=0\implies y^4-6y^2+1=0\implies y^2=3+2\sqrt 2\implies |z|_{max}=\sqrt {3+2\sqrt 2}=\sqrt 2+1\approx \boxed {2.4142135623731}$ .