Maximum Permutation

We claim that $\max\left(\displaystyle\min_{1\le i\le 999} |\sigma(i+1)-\sigma(i)|\right)=499$ for all permutations $\sigma$ . We shall now prove this statement.

Consider $i$ such that $\sigma(i)=500$ . Clearly, $\sigma(i+1)$ and $\sigma(i-1)$ must be chosen from the $998$ remaining numbers. But the maximum value for the expression occurs for $\{\sigma(i-1),\sigma(i+1)\}\in \{1,999\}$ , and thus we can conclude that $\min|\sigma(i+1)-\sigma(i)|\le 499$ .

Now, it remains to construct a permutation which satisfies $\displaystyle\min_{1\le i\le 999}|\sigma(i+1)-\sigma(i)|= 499$ . This is relatively easy:

$(\sigma(1),\sigma(2), \sigma(3), \ldots, \sigma(999))=(1,501,2,502,\ldots ,499, 999,500)$ .

To show that $499$ is attainable, we can let $\sigma(2i-1)=501-i$ . for $i=1,2,\ldots,500$ and $\sigma(2i)=1000-i$ for $i=1,2,\ldots,499$ . So $|\sigma(2i+1)-\sigma(2i)|=1000-i-500+i=500$ and $|\sigma(2i)-\sigma(2i-1)|=1000-i-501+i=499$ .

To show $499$ is upper bound, let $\sigma(k)=500$ and choose one of the numbers $\sigma(k-1)$ and $\sigma(k+1)$ , since for $k\in[1,999]$ one of $k-1,k+1$ also lie in the same interval. Let $a\in[1,999]$ with $|k-a|=1,$ if $|500-\sigma(a)|>499$ , $\sigma(a)<1$ or $\sigma(a)>999$ , contradiction. So $\min{|\sigma (i+1)-\sigma (i)|}\le 499$ . With the example above we know that the answer is $499.$

499 is possible, demonstrated by: 1,501,2,502,...,500,1000. To prove 500 or any number greater than 500 aren't possible, just look at the number 500. As its both neighbours differ by at least 500 from 500, we infer that its neighbours are less than 1 or at least 1000 - not possible.

For those who do not understand the question, this is the explanation:

Think of all the distinct circular arrangements of the integers from 1 to 999. If you want to know how many arrangements there are, it is exactly (999-1)! or 998! each consisting of 999 integers. You don't want to stick with trial and error, which requires listing. Now, as said in the problem, \sigma (1000) = \sigma (1) so to avoid being confused, it is safe to assume that the arrangement is circular. Now, for each of the 998! arrangements, you have to think of the maximum value of \displaystyle \min_{1 \leq i \leq 999} |\sigma(i+1)-\sigma(i)|. It basically means you have to think the maximum value of the absolute value of the difference between any two consecutive integers in all the 998! arrangements. Then, assuming that you have the maximum value in each of the 998! arrangements, the answer is the least one.

Now that you understood the problem, you can answer it by critical thinking. Keep in mind that the arrangement is circular, so the identity permutation has a maximum value of \displaystyle \min {1 \leq i \leq 999} |\sigma(i+1)-\sigma(i)| of 998, because 1 and 999 are next to each other, hence the circular arrangement. What you have to think is to make the value of \displaystyle \min {1 \leq i \leq 999} |\sigma(i+1)-\sigma(i)| almost equal in just one arrangement, so that there will be no high value such as 998 in the identity permutation. That is the only time that you will obtain the least maximum value over all permutations. If you truly understood the conditions I stated, you will eventually come up with the circular arrangement of { 500, 999, 499, 998, 498, 997, 497, 996, ... , 3, 502, 2, 501, 1 } and the absolute value of the differences between any two consecutive integers will be 499 and 500.

Therefore, the maximum value over all permutations of \displaystyle \min_{1 \leq i \leq 999} |\sigma(i+1)-\sigma(i)| = 499.

Consider $k$ such that $\sigma(k) = 500$ . Then, $|\sigma(k+1)-\sigma(k)| \leq 499$ , so the minimum is at most 499. We show that it is possible to have a permutation where the minimum is 499. If any of the numbers from 2 to 500 are beside each other, then $|\sigma(k+1)-\sigma(k)| < 499$ . So we place them one apart from each other like this: $\sigma(2) = 2, \sigma(4) = 3, \sigma(6) = 4 \ldots \sigma(998) = 500$ . We notice that $i + 499$ gives the numbers from 501 to 999 for $2 \leq i \leq 500$ . Thus, we place $i+499$ on the left of where $i$ is placed: $501, 2, 502, 3, \ldots 999, 500$ . We can place 1 in the last spot and it would be valid as $501 - 1 = 500$ and $500 - 1 = 499$ . Thus, the series would be $501, 2, 502, 3, \ldots 499, 999, 500, 1$ and it satisfies $|\sigma(i+1) - \sigma(i)| \leq 499$ for $1\leq i \leq 999$ . This series is not unique as we can shift the entire series one place to the right and place 1 at the front. We can also reverse the series and the property will still hold.

There is a graph-ish way to interpret the problem: let $G=(V,E)$ be an undirected graph such that each vertex $v_i \in V$ represents a number in $\{1,2,...,n\}$ and an edge $(v_i, v_j) \in E$ exists if $v_i$ and $v_j$ are adjacent in $\sigma$ . The weight on each edge is $w_{ij}=|v_i - v_j|$ .

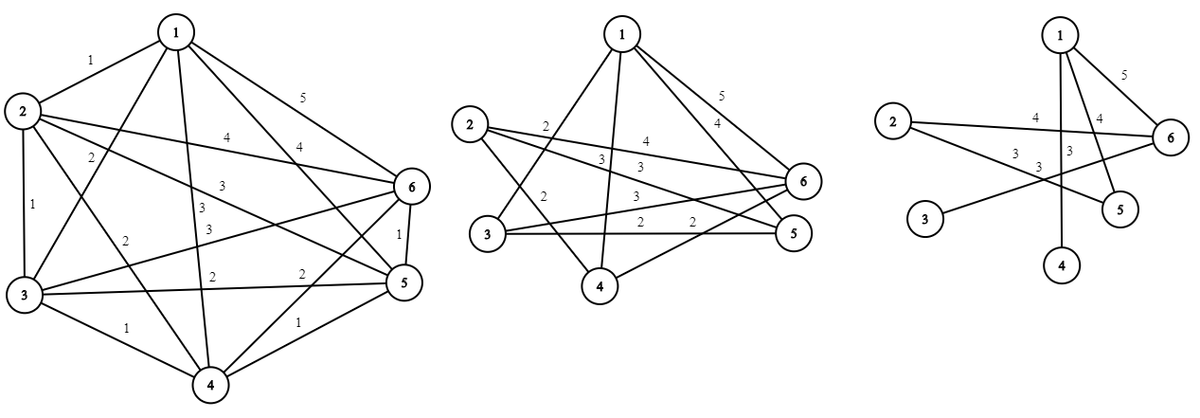
The process consists of removing all edges $\displaystyle \{(v_i, v_j) \ | \ w_{ij} = \min_{i,j} w_{ij}\}$ under the condition that the $G$ remains connected. The figure shows an example for $n=6$ . I don't know if there's a way to prove that the vertex $\lceil n/2\rceil$ is the one that ends up having all of its edges with the minimum weight value (in graph theory terms). If that is the case, the solution for the problem is $n - \lceil n/2 \rceil = \lfloor n/2 \rfloor$

Define the multiset S which contains each integer from 1 to 500 exactly twice. S has exactly 1000 elements. Consider each pair of integers (sigma(i+1), sigma(i)) as i ranges from 1 to 999. These pairs cover sigma(i) twice for each i from 1 to 999, thus S is covered by the 999 pairs. By pigeonhole principle, some pair contains 2 elements of S. The largest possible difference of that pair is 500 - 1 = 499.

construction:500,999,499,998,498,997,……2,501,1

The key is noting that if $\sigma(a) = 500$ and $a < 999$ (if $a = 999$ , reverse the permutation so $a = 1$ ), we have:

$1-500 = -499 \le \sigma(a+1) - \sigma(a) \le 499 = 999-500$

$|\sigma(a+1) - \sigma(a)| \le 499$

So $\displaystyle\min_{1 \le i \le 998} |\sigma(i+1) - \sigma(i)| \le |\sigma(a+1) - \sigma(a)| \le 499$ .

Achieving this bound is simple though, seeing that $499$ is nearly half of $999$ : $\sigma = (500, 1, 501, 2, 502, 3, \ldots, 998, 499, 999)$ achieves the bound.

So the answer is $499$ .

We can consider this permutation as a cycle of numbers starting from 500, since the 1000th term is the 1st term, making it a cycle and it can start with any number since it is a cycle. First we show the answer 499 is valid by choosing $500,1,501,2,502\ldots 499, 999$ . Then assume the answer is at least 500, then starting with 500, we have no valid number to follow. The answer is therefore 499.

We know that $\sigma(i)=500$ for some $i \in \{1,2,3, \ldots, 999 \}$ . So, $|\sigma (i+1)-\sigma (i)| \leq 499$ . Hence, the value over all permutations of $\min_{1 \leq i \leq 999} |\sigma (i+1) - \sigma (i)| \leq 499$ . The maximum value of $499$ can be attained using the order $\{1,501,2,502, \ldots, 499,999,500 \}$ .