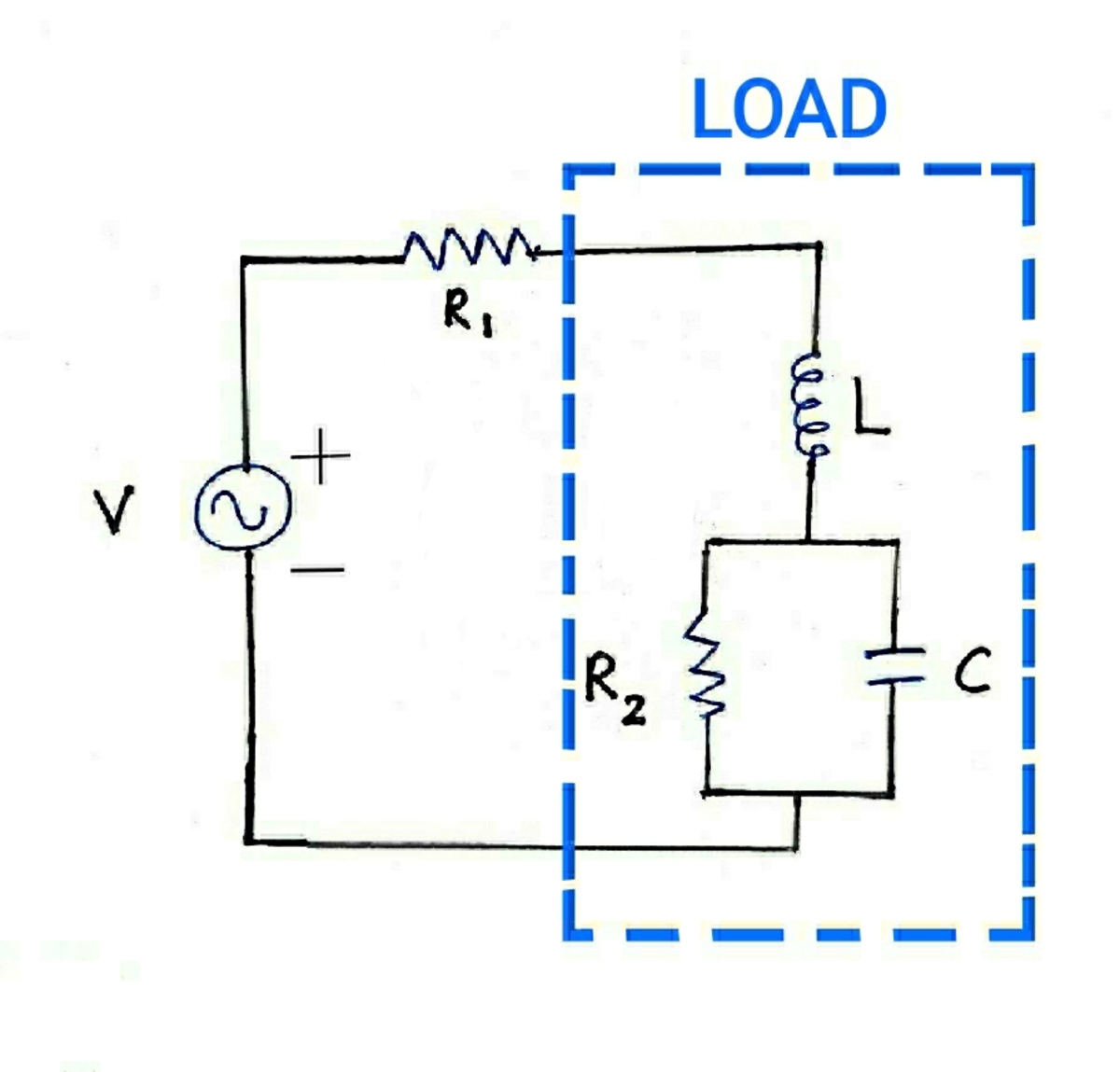
Maximum Power Transfer

Interesting problem for the harmonic steady state! Before we begin, we normalize all currents, voltages, time and elements by the values given below: $\begin{aligned} \text{voltages:}&&&\SI{1}{V}, &&&\text{currents:}&&&\SI{1}{A},&&&\text{time:}&&&\SI{1}{s}&&& \Rightarrow &&&&R:&&&\SI{1}{\ohm}, &&& C:&&&\SI{1}{F}, &&&L:&&&\SI{1}{H},&&&P:&&&\SI{1}{W} \end{aligned}$ The network equations remain the same in the process, but now all currents, voltages, time and elements represent their normalized dimensionless counterparts.

---

Remember in single frequency harmonic steady state, the average power consumed in a (load) impedance $Z_L$ is

$\begin{aligned} P&=\frac{1}{2}\Re\{U_L I_L^*\}=\frac{|I_L|^2}{2}\Re(Z_L\}, &&&&&U_L:&\text{ pointer of voltage over }Z_L, &&&I_L:&\text{ pointer of current through }Z_L \end{aligned}$

In the given network, our load impedance consists of $R_2,\:C,\:L$ . We split it into real- and imaginary part: $\begin{aligned} Z_L&=j\omega L + R_2\|\frac{1}{j\omega C}=j\omega L + \frac{R_2}{j\omega R_2C + 1} = j\omega L + \frac{R_2 - j\omega R_2^2C}{|j\omega R_2C+1|^2} & (*) \end{aligned}$ We assume both $U_L,\:I_L$ are oriented downward. By Kirchhoff's Voltage Law (KVL) we get $\begin{aligned} I_L&=\frac{V}{R_1+Z_L} &&&\Rightarrow &&&& P&=\frac{|I_L|^2}{2}\Re\{Z_L\} \underset{(*)}{=} \frac{|V|^2}{ 2|R_1+Z_L|^2 }\cdot\frac{R_2}{ |j\omega R_2C_2 + 1|^2 } = \frac{|V|^2R_2}{ 2|(j\omega L + R_1)(j\omega R_2C+1) + R_2|^2 }\\[1em] &&&&&&&&& = \frac{|V|^2R_2\cdot |-j\omega L+R_1|^2}{ 2\left||j\omega L+R_1|^2(j\omega R_2C+1) + R_2(-j\omega L+R_1)\right|^2 }=:\frac{\text{const}}{2Q(C)} \end{aligned}$ Only the denominator still depends on $C$ . If we want to maximize $P$ , we need to minimize $Q(C)$ : $Q(C) = \left(|j\omega L+R_1|^2\omega R_2C-\omega R_2L\right)^2 + \left(|j\omega L+R_1|^2 + R_1R_2\right)^2\geq \left(|j\omega L+R_1|^2 + R_1R_2\right)^2$ The denominator $Q(C)$ can reach its minimum if (and only if) the first square vanishes. As long as $|j\omega L+R_1|^2\omega R_2\neq 0$ , we get $\begin{aligned} |j\omega L+R_1|^2\omega R_2C-\omega R_2L&\overset{!}{=}0 &&&\Rightarrow &&&& C&=\frac{L}{|j\omega L+R_1|^2} = \frac{5\cdot 10^{-3}}{|j0.5+0.5|^2}=10^{-2},& 1000C&=\boxed{10} \end{aligned}$