maximum power transfer........
Electricity and Magnetism
Level
3
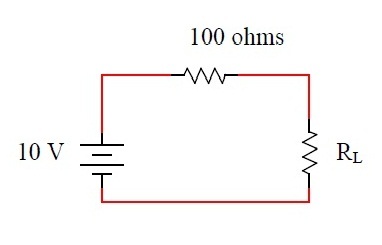 The maximum power that can be transferred to the load resister RL from the voltage source in fig is
The maximum power that can be transferred to the load resister RL from the voltage source in fig is
1 W
10 W
0.25 W
0.5 W
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
It is textbook's stuff that the maximum power transferred occurred when the load resistance R L is equal to that of the resistance of the series resistor R S (sometimes the internal resistance of the voltage source), 1 0 0 Ω . When R L = 1 0 0 Ω , then the current
I = 1 0 0 Ω + 1 0 0 Ω 1 0 V = 0 . 0 5 A .
Therefore the maximum power transferred is:
P m a x = I 2 R L = 0 . 0 5 2 × 1 0 0 = 2 . 5 W .
Proof:
P R L = I 2 R L = ( R L + R S V ) 2 R L
d R L d P R L = d R L d ( ( R L + R S ) 2 V 2 R L )
= V 2 ( ( R L + R S ) 2 1 − ( R L + R S ) 3 2 R L )
= V 2 ( ( R L + R S ) 3 R L + R S − 2 R L )
= V 2 ( ( R L + R S ) 3 R S − R L )
P R L = P m a x when d R L d P R L = 0 or when R L = R S .