Maximum segment for circles points

Here $BE^2+BF^2=EF^2$ - and max $EF$ for $BE=2r_1=15$ and $BF=2r_2=20$ . Answer $\sqrt{15^2+20^2}=25$ .

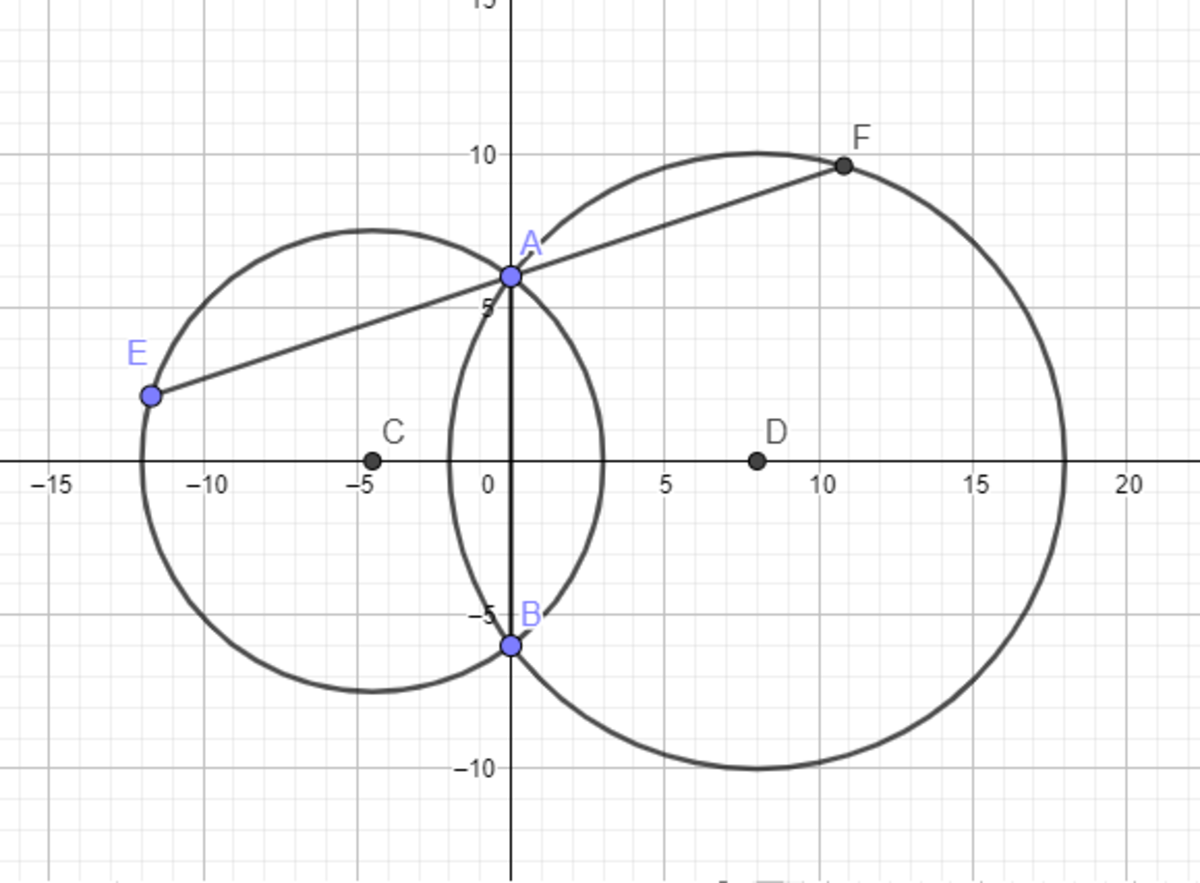
Using the graph given by @Yurly Kazokov , the equations of the two circles are:

$\begin{cases} C_1: & (x-8)^2 + y^2 = 10^2 & \implies y^2 = 36 - x^2 + 16x & ...(1) \\ C_2: & (x+4.5)^2 + y^2 = 7.5^2 & \implies y^2 = 36 - x^2 - 9x & ...(2) \end{cases}$

Let the equation of segment $EF$ be $y = mx + 6$ , where $m$ is the gradient of the line. Then $y^2 = m^2x^2 + 12mx + 36$ . Now let $E(x_2,y_2)$ and $F(x_1,y_1$ and we have:

$\begin{cases} m^2x_1^2 + 12mx_1 + 36 = 36 - x_1^2 + 16x_1 & \implies x_1 & = \dfrac {16-12m}{m^2+1} \\ m^2x_2^2 + 12mx_2 + 36 = 36 - x_2^2 - 9x_2 & \implies x_2 & = \dfrac {-9-12m}{m^2+1} \end{cases}$

Now the length of $EF$ is given by:

$\begin{aligned} |EF| & = \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2} = \sqrt{(x_1-x_2)^2 + m^2(x_1-y_2)^2} \\ & = (x_1-x_2)\sqrt{1+m^2} = \frac {16-12m +9 + 12m}{m^2+1} \sqrt{1+m^2} \\ & = \frac {25}{\sqrt{m^2+1}} \end{aligned}$

$|EF|$ is maximum when $m=0$ , that is when $EF$ is parallel to the $x$ -axis, and $|EF|_{\text{max}} = \boxed{25}$ .

$let \ \theta = \angle CEA = \angle CAE \\ {\color{#D61F06} \Rightarrow \angle ECA = 180 - 2 \theta} \\ \triangle CAD \ is \ right \ triangle \Rightarrow \angle DAF = \angle DFA = 90 - \theta \\ {\color{#D61F06} \Rightarrow \angle ECA = 2 \theta}$

Now using Law of Cosines

\(\begin{align} \left | EA \right |^2 &= \left | CE \right |^2 + \left | CA \right |^2 - 2 \cdot \left | CE \right |\cdot \left | CA \right | \cdot {\color{blue} \cos(180 - 2 \theta)} \\ \left | EA \right |^2 &= \frac{225}{2} \left ( 1+ {\color{blue} \cos(2 \theta)} \right ) = 225\left ( \frac{1+\cos(2 \theta)}{2} \right ) = 225 \cos^2(\theta)\\ \left | EA \right | &= 15 \cos(\theta) {\color{red} \rightarrow 1} \\

\left | AF \right |^2 &= \left | AD\right |^2 + \left | FD\right |^2 - 2 \cdot \left | AD\right |\cdot \left | FD\right | \cdot \cos(2 \theta) \\ \left | AF \right |^2 &= 200\left ( 1 - \cos(2 \theta) \right ) = 400\left ( \frac{1-\cos(2 \theta)}{2} \right ) = 400\sin^2(\theta)\\ \left | EA \right | &= 20 \sin(\theta) {\color{red} \rightarrow 2} \\

\left | EF \right | &= \left | EA \right | + \left | AF \right | \\ \left | EF \right | &= 20 \sin(\theta) + 15 \cos(\theta) \\ \frac{d}{d \theta} \left | EF \right | &= 20 \cos(\theta) - 15 \sin(\theta) = 0 \\ & {\color{blue} \Rightarrow \tan(\theta)=\frac{4}{3}} \\

\frac{d^2}{d \theta^2} \left | EF \right | &= -20 \sin(\theta) - 15 \cos(\theta) < 0 {\color{blue} \ when \ 0<\theta<90} \\ & {\color{blue} \tan(\theta)=\frac{4}{3} \Rightarrow \left | EF \right | \ is \ max} \\

& \tan(\theta)=\frac{4}{3}\Rightarrow \sin(\theta) = \frac{4}{5} ;\cos(\theta) = \frac{3}{5} \\ \left | EF \right | &= 20 \sin(\theta) + 15 \cos(\theta) \\ \left | EF \right | &= 20 \cdot \frac{4}{5} + 15 \cdot \frac{3}{5} = 25 \end{align} \)

Let $G$ be the point of intersection of $AB$ and $CD$ . Then, $G$ is the midpoint of $AB$ . Applying Pythagoras theorem on $\triangle ACG$ and $\triangle ADG$ we find that $CG=4.5$ and $GD=8$ , thus $CD=12.5$ .

Let $CH$ , $DI$ be the apothems of the cords $EA$ , $AF$ respectively and $CJ\bot DI$ .

$\ \$

Suppose $EF$ is not parallel to $CD$ . Then, $EF=2HI=2CJ<2CD\implies EF<25.$

$\ \$

In case $EF\parallel CD$ , $\triangle CDJ$ degenerates into the line segment $CD$ and $EF=2CD=25.$

$\ \$

Hence, the longest segment $EF$ is the one that is parallel to the diacenter $CD$ and its length is $\boxed{25}.$

Horizontal segment is found to have maximum length as on both other sides the length reduces. Take a line y=mx +b passing through point A and calculate

EF=2CD/(1+m^2)^0.5

EF_Max=2CD, for this problem CD=12.5

Answer is 25

The question didn't give any significant coordinates for E and F points.That means wherever you rotate it, the length of the given EF line must remain same. By this method rotate the line to make it parallel to x-axis.Now you can calculate it easily.