Maximum surface area of a variable polyhedron
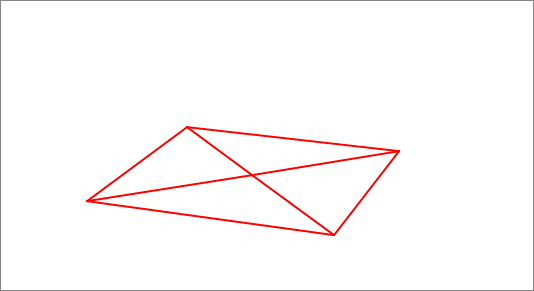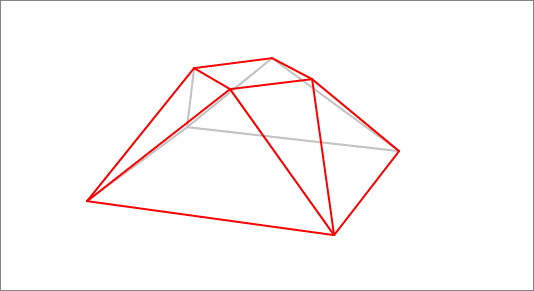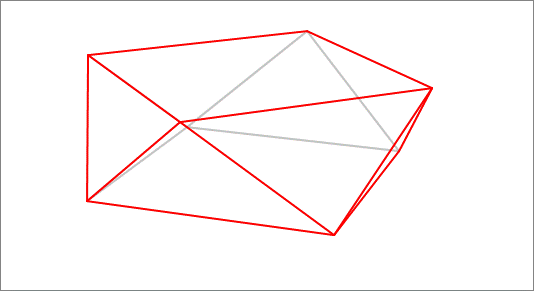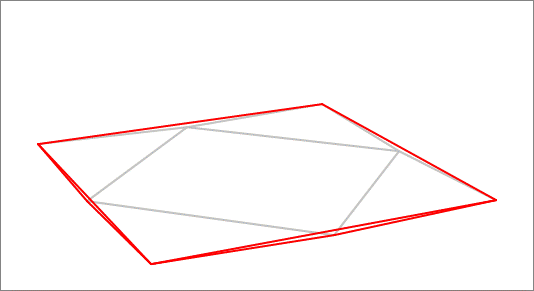
A variable polyhedron is constructed from a square of side length , by rotating (copies of) its center about each of its four sides by the same angle, and then generating the convex polyhedron connecting the resulting vertices, as shown in the above animation. Find the maximum possible surface area of this variable polyhedron.
The answer is 441.42.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The surface area A of the polyhedron only depends on the side length of the top square x . It has a minimum of 2 0 0 when x = 0 . The additional surface area is the square on top x 2 and the area of the four slanting triangles which we can find using Heron's formula , where its semi-perimeter s = 2 5 2 + 5 2 + x = 5 2 + 2 x . The surface area A is given by:
A d x d A = x 2 + 4 ( 5 2 + 2 x ) ( 5 2 − 2 x ) ( 2 x ) 2 + 2 0 0 = x 2 + x 2 0 0 − x 2 + 2 0 0 = 2 x + x 2 0 0 − x 2 2 0 0 x − 2 x 3 = 2 0 0 − x 2 2 x 2 0 0 − x 2 + 2 0 0 − 2 x 2 To find max ( A ) Putting d x d A = 0
2 x 2 0 0 − x 2 x 2 0 0 − x 2 2 0 0 x 2 − x 4 2 x 4 − 4 0 0 x 2 + 1 0 0 0 0 x 4 − 2 0 0 x 2 + 5 0 0 0 = 2 x 2 − 2 0 0 = x 2 − 1 0 0 = x 4 − 2 0 0 x 2 + 1 0 0 0 0 = 0 = 0
⟹ x 2 x = 2 ± 2 0 0 2 − 4 ( 5 0 0 0 ) + 2 0 0 = ± 5 0 2 + 1 0 0 = 1 0 0 ( 1 + 2 1 ) = 1 0 1 + 2 1 1 0 0 − 5 0 2 is too small.
⟹ A max = 1 0 0 ( 1 + 2 1 ) + 1 0 1 + 2 1 ⋅ 2 0 0 − 5 0 2 − 1 0 0 + 2 0 0 = 2 0 0 + 5 0 2 + 1 0 1 + 2 1 ⋅ 1 0 0 − 5 0 2 = 3 0 0 + 2 1 0 0 + 1 0 1 + 2 1 ⋅ 1 0 1 − 2 1 = 3 0 0 + 2 1 0 0 + 2 1 0 0 = 3 0 0 + 1 0 0 2 ≈ 4 4 1 . 4 2