System of Circle-O-Triangle!

Geometry Level 5

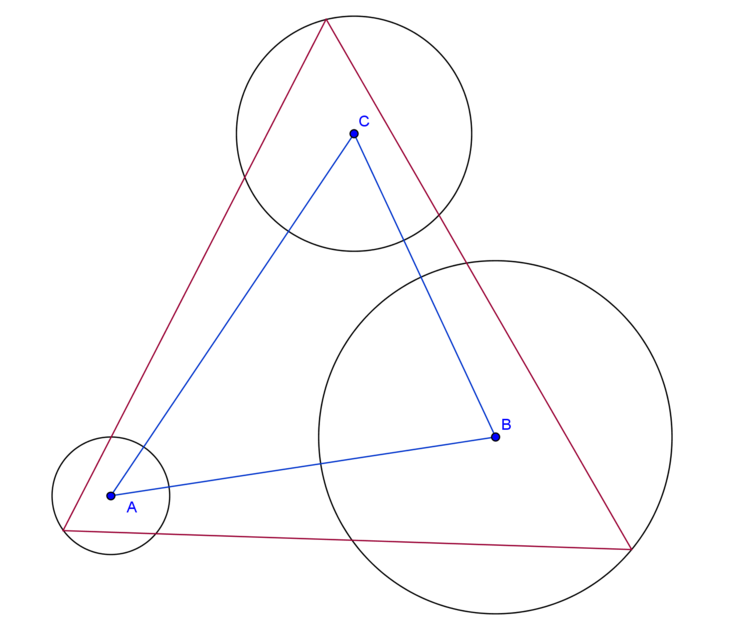There are 3 circles.

  • First one has center at A ( 3 2 , 0 ) A \left(\dfrac{\sqrt{3}}{2},\ 0 \right) and has radius 1 1 .

  • Second one has center at B ( 20 − 3 3 2 , 1 ) B \left(\dfrac{20-3\sqrt{3}}{2},\ 1 \right) and has radius 3 3 .

  • Third one has center at C ( 5 , 5 3 − 3 2 ) C \left(5,\ 5\sqrt{3}-\dfrac{3}{2} \right) and has radius 2 2 .

Find the perimeter of the triangle with maximum area, having one vertex on the circumference of each of the circles. Enter the answer to 3 decimal places.


The answer is 31.743.

Maria Kozlowska by Maria Kozlowska , 57, Canada

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Maria Kozlowska
Sep 19, 2015

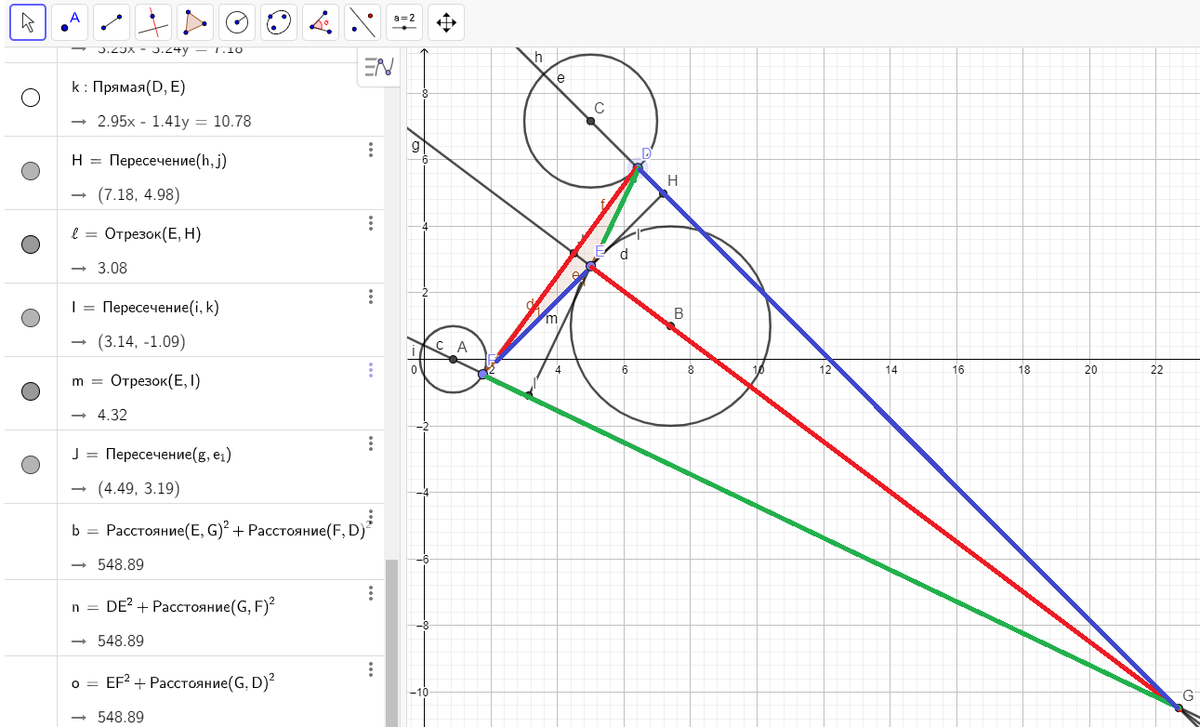
The maximum area is obtained when altitudes of the new triangle pass through the center points of the three circles. The are few methods to get the result.

1) Equation for triangle area using unknown vertex coordinates. To reduce number of unknown values substitution can be made using equations of the circles. This way we get equation for the area with 3 unknowns. Differentiation by each unknown equated to 0 gets us 3 equations which solved would give us vertex coordinates and perimeter.

2) There is an equation for general point on an altitude: if E is any point on an altitude AD of any triangle ABC, then:

A C 2 + E B 2 = A B 2 + C E 2 AC^2+EB^2=AB^2+CE^2

Each of the circle centres can be used in this equation as a point on an altitude. Solving these equations would give us vertex coordinates.

Note: If someone has an idea for geometric construction for this type of problem, please post.

1 Helpful 0 Interesting 0 Brilliant 0 Confused

Thanks. I have updated the answer to 31.743. Those who answered 31 or 32 (when the answer had to be an integer) were marked correct.

In future, to request a change in the answer, please report the problem. We respond immediately (24 hours) to reports posted by the problem creator, and deal with them accordingly.

Can you edit in the solution? Thanks!

Calvin Lin Staff - 5 years, 8 months ago

Interesting problem. Here 2.48151 - it is min Tringle Area for this cicrles. The same conditions work for min Tringle Area - see Geogebra picture

Yuriy Kazakov - 1 year ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...