Maximum Value

Using Cauchy-Schwarz inequality, we have:

$(ab+bc+ca)^2 \le (a^2+b^2+c^2)(b^2+c^2+a^2) = (a^2+b^2+c^2)^2$

$\Rightarrow ab+bc+ca \le a^2+b^2+c^2 = (a+b+c)^2-2(ab+bc+ca)$

$\Rightarrow 3(ab+bc+ca) \le (a+b+c)^2$

$\Rightarrow ab+bc+ca \le \dfrac {(a+b+c)^2}{3} = \dfrac {16}{3}$

Therefore, the required answer $x \times y = 16 \times 3 = \boxed{48}$

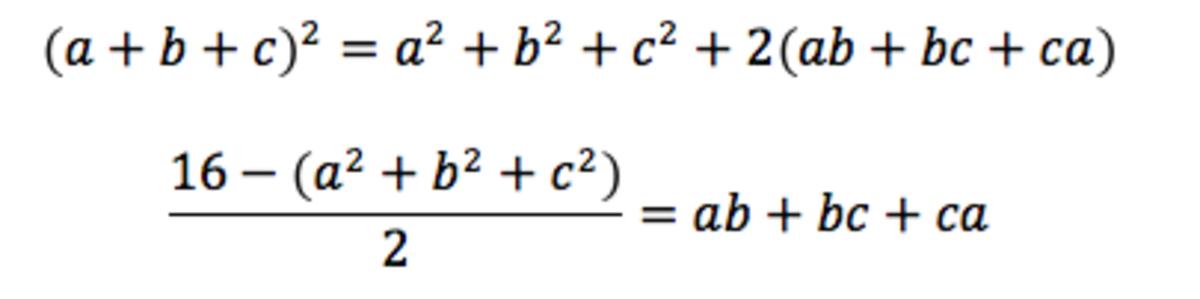In order to find the maximum value we have to minimize the expresion in the parenthesis.

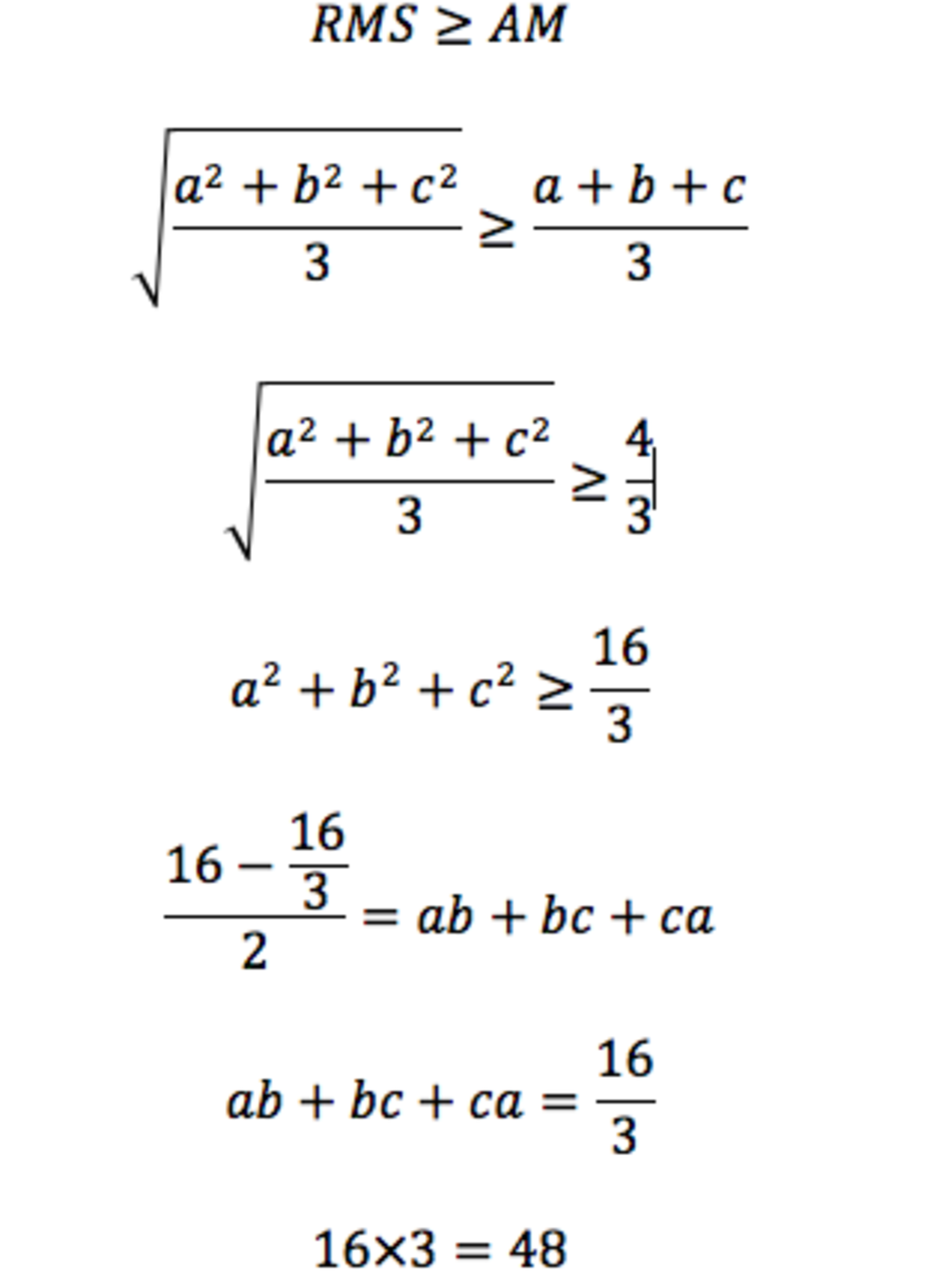
Let's assume that $a>b>c$

Then aplly $\color{#E81990}{Re-arrangement Inequality}$ to get.

$ab+bc+ca \leq a^{2}+b^{2}+c^{2}$

$\Rightarrow ab+bc+ca \leq (a+b+c)^{2}-2\times(ab+bc+ca)$

$\Rightarrow 3\times(ab+bc+ca) \leq(a+b+c)^{2}$

So $ab+bc+ca\leq\dfrac{(a+b+c)^{2}}{3}$

By this $\large |ab+bc+ca|_{max}=\dfrac{16}{3}$

So the answer is $\large 16 \times 3=48$

This occurs when $a=b=c=\dfrac{4}{3}$

Using AM-GM, we have:

$a+b+c\geq3\sqrt[3]{abc}\Rightarrow abc\leq(\frac{4}{3})^3$

Now, $(a+1)+(b+1)+(c+1)=7$

$(a+1)+(b+1)+(c+1)\geq3\sqrt[3]{(a+1)(b+1)(c+1)}$

$(\frac{7}{3})^3\geq abc+(ab+ac+bc)+(a+b+c)+1$

$(\frac{7}{3})^3-(\frac{4}{3})^3-4-1\geq ab+ac+bc$

$ab+ac+bc\leq \frac{16}{3}$

So, the answer is $x\times{y}=16\times{3}=\boxed{48}$

i used cauchy schwartz inequality

(aa+bb+cc)(bb+cc+aa)>= (ab+bc+ca)^2

(aa+bb+cc)^2>= (ab+bc+ca)^2

(aa+bb+cc)>= (ab+bc+ca)..........-ve rejected bcoz all r positive

(a+b+c)^2-2(ab+bc+ca) >= (ab+bc+ca)

rearrage to get

16/3 >= (ab+bc+ca) ...........ANS

Try out a=b=c=4/3. Say we decrees one and increase the other by same amount to maintain the total at 4. Take a=b=c=4/3 and (a+d), (b-a), and c, as new numbers. (a+d) + (b-a) + c = k>0.

So c{(a+d)+(b-d)}+(a+d) (b-d) =c( a +b) +ab + d(b-a) -d d= ab +bc + ca -d*d.
SO UNLESS d = 0, all other values will make ab +bc + ca small. a, b, c may be
ANY real number.
$\large \color{#3D99F6}{~~For~~ANY~~real~~a, ~b,~ c, ~k,~~~~IF~~a+b+c=k,~\\ maximum~ ab+bc+ca=\dfrac{k^2}{3}~~when ~~a=b=c=\dfrac{k}{3}.}\\So~~our~~answer~~is~~~~~~~\boxed {\color{#D61F06}{ \large ~~~~48~~~~}}\\ ~~\\$

Can k be any real number, not only k>0 ? Any one has an answer ?

The maximum value will only come when there is equality... That is a=b=c=4/3...si maximum value of ab+bc+ca=16/9*3=16/3...implies x=16 y=3 implies xy=48

I recognized that a, b, and c were symmetric variables so the maximum would occur when they were all equal at 4/3. Simply substituting gives ab+bc+ac=16/3.