Maximum value in triangle#1
In the triangle , , and are the radii of the circles that inscribes and circumscribes triangle respectively.
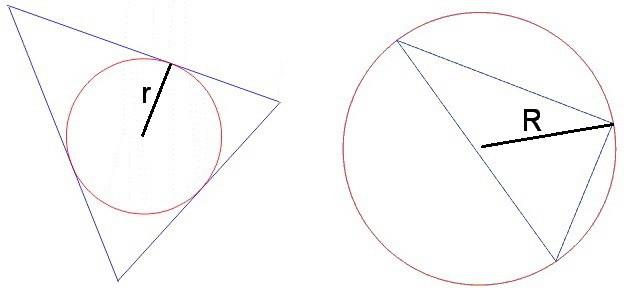
If and , find the maximum value of .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
There are 2 formulas related to r and R should be using:
+) The radius of triangle's incircle is given by
r = P e r i m e t e r 2 × A r e a = a + b + c 2 p ( p − a ) ( p − b ) ( p − c ) (applying Heron's Formula for the area of a triangle where p is half the perimeter, or 2 a + b + c )
⟹ r = 2 1 a + b + c ( b + c − a ) ( a + c − b ) ( a + b − c )
+) The radius of triangle's circumcircle is given by
R = ( a + b + c ) ( b + c − a ) ( a + c − b ) ( a + b − c ) a b c
From 2 above formulas, R r = a b c ( b + c − a ) ( a + c − b ) ( a + b − c )
Let f ( c ) = a b c ( b + c − a ) ( a + c − b ) ( a + b − c )
⟹ f ′ ( c ) = 2 a b c 2 ( a + b ) c 2 − 2 c 3 + ( a + b ) ( a − b ) 2 ≥ 2 a b c 2 ( a + b − 2 c ) c 2 > 0
So, f ( c ) is increasing in term of c .
Since a + b ≥ 3 c ⟹ c ≤ 3 a + b
⟹ f ( c ) ≤ f ( 3 a + b ) = 9 a b 4 ( 2 b − a ) ( 2 a − b ) = 9 4 − 9 a b 2 ( a − b ) 2 ≤ 9 4 , or R r ≤ 9 4
We then have ( R r ) m a x = 9 4 when a = b = 2 3 c .