Maximum Value of Infinite Series with Trigonometric terms.
Geometry
Level
3
Calculate the maximum value of this Infinite series
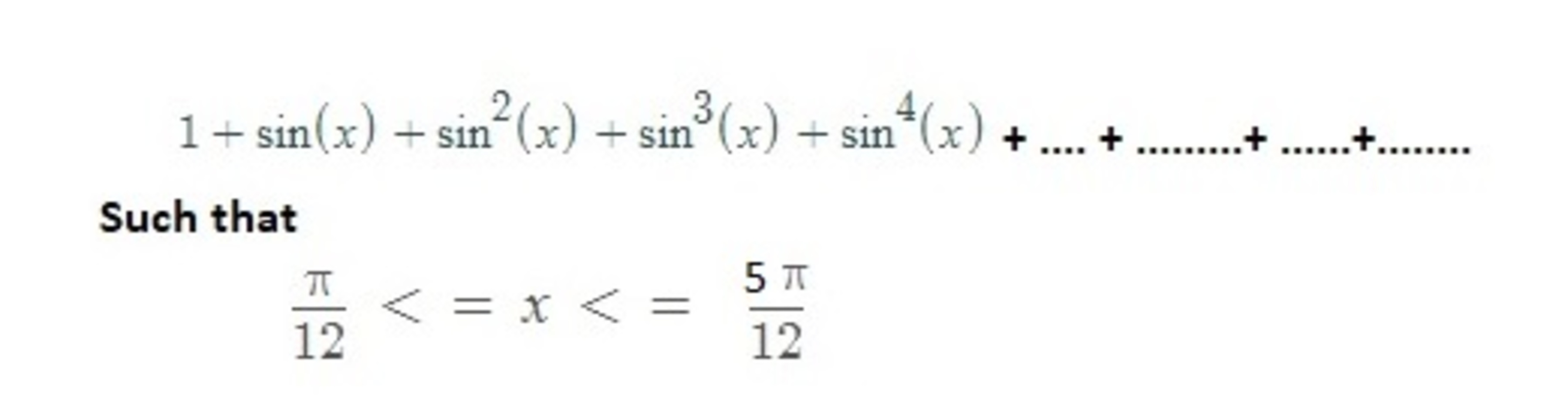
The answer is 29.347.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Within the given range of x , Sin(x) is less than 1 and greater than 0. The sum of this infinte series can be calculated using the fact that this is an infinite geometric progression with Sin(x). So the sum of all terms is 1/ (1-Sin(x)).
Since Sin(x) is increasing in the given interval , the maximum value of (1/1-Sin(x)) occurs at x = 5 * pi/12.
Sin (5 pi/2) can be calculated as Sin(pi/6 + pi/4) = Sin pi/6 * Cos(pi/4) + Cos(pi/6) Sin(pi/4) = 1/sqrt(2)(0.5 + 0.866) = 0.96592583
The maximum value of the infinite series is hence equal to 1/(1 - 0.96592583) = 29.3477