Maximum volume of a cone
An open-top cone has a surface area of 100. What is the maximum possible volume that the cone can hold?
The answer is 116.675.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
An AM-GM solution for a calculus question? +1
Log in to reply
This is only one solution of this problem. We also can solve it by Calculus approachs such as using Lagrange multipliers, using derivative to find extrema of a function of one variable. These approachs could be more natural, so I set this question is a calculus question.
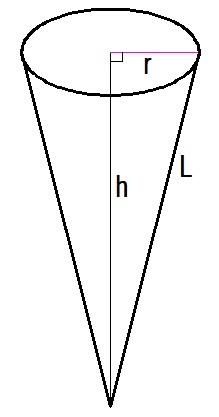 For maximum volume of a right circular cone (open on top),
h
=
r
2
.
For maximum volume of a right circular cone (open on top),
h
=
r
2
.
L = h 2 + r 2 = 2 r 2 + r 2 = r 3
The lateral area of the cone is given by A = 2 1 c L where c is the circumference of the base and L is the slant height. We have
1 0 0 = 2 1 ( 2 π r ) ( r 3 )
r 2 = 3 π 1 0 0 or r = 3 π 1 0 0 = 3 π 1 0
The volume of a cone is given by V = 3 1 A b h where A b is the area of the base and h is the height. We have
V = 3 1 ( π ) ( 3 π 1 0 0 ) ( 3 π 1 0 2 ) ≈ 1 1 6 . 6 7 5
If the radius of the base is r and the height is h the volume of the cone is 3 1 π r 2 h and the surface area (excluding the base) is π r r 2 + h 2 .
From the hypothesis, we have π r r 2 + h 2 = 1 0 0 . And we must find the maximum value of 3 1 π r 2 h .
Appying the AM-GM inequality, we have: r 2 + h 2 = r 2 + 2 h 2 + 2 h 2 ≥ 3 3 4 r 2 h 4 Hence, 1 0 0 = π r r 2 + h 2 ≥ π r ⋅ 3 3 2 r h 2 = π 3 3 2 r 4 h 2
This implies that r 4 h 2 ≤ 2 ( π 3 1 0 0 ) 3 = 3 π 3 3 2 ⋅ 1 0 6 or r 2 h ≤ π π ⋅ 4 2 7 1 0 0 0 2
So, 3 1 π r 2 h ≤ 3 π ⋅ 4 2 7 1 0 0 0 2 ≈ 1 1 6 . 6 7 5 .
The inequality holds if and only if h = r 2 = π ⋅ 4 3 1 0 2 .