Maxwell was right!

Electricity and Magnetism Level 3

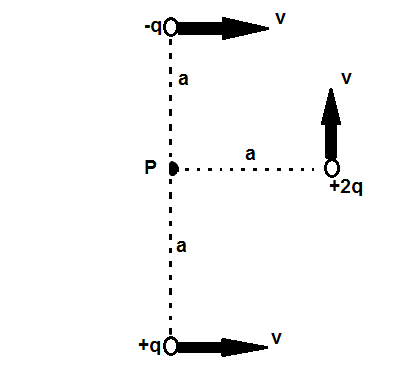A charge $+2q$ moves vertically upwards with speed $v$ , a second charge $-q$ moves horizontally to the right with the same speed $v$ , and a third charge $+q$ moves horizontally to the right with the same speed $v$ . The point P is located a perpendicular distance $a$ away from each charge as shown in figure. What is the magnetic field at point P?

Details and Assumptions

$-\hat{k}$ denotes into the page and $\hat{k}$ denotes out of the page.

Try my set .

\dfrac{\mu_0 2qv}{4\pi a^2} \hat{k}

\dfrac{\mu_0 4qv}{4\pi a^2} \hat{k}

\dfrac{\mu_0 4qv}{4\pi a^2} -\hat{k}

\dfrac{\mu_0 2qv}{4\pi a^2} -\hat{k}

1 solution

Vishwak Srinivasan
Jul 6, 2015

The Biot Savart Law, can also be written in the way below

$\vec{dB} = \dfrac{\mu_0 dq (\vec{v} \times \hat{r})}{4\pi r^2}$

The above formula can be derived by using the concept of drift velocity.

For all the charges, the direction of magnetic field induced by it is out of the page, i.e., $\hat{k}$ .

For the each charge, the magnitude of magnetic field induced is

$|B_{+2q}| = \dfrac{\mu_0 2q v}{4\pi a^2}$

$|B_{+q}| = \dfrac{\mu_0 q v}{4\pi a^2}$

$|B_{-q}| = \dfrac{\mu_0 q v}{4\pi a^2}$

The net magnitude of magnetic field induced at P $= \dfrac{\mu_0 4qv}{4\pi a^2}$ .

Hence the magnetic field induced at point P is $\boxed{\dfrac{\mu_0 4qv}{4\pi a^2} \hat{k}}$

Exactly.Nice and easy solution. I did in the same manner.

Saaket Sharma - 5 years, 10 months ago

Maxwell was right!

Try my set .

1 solution

0 pending reports