Maybe, Maybe not

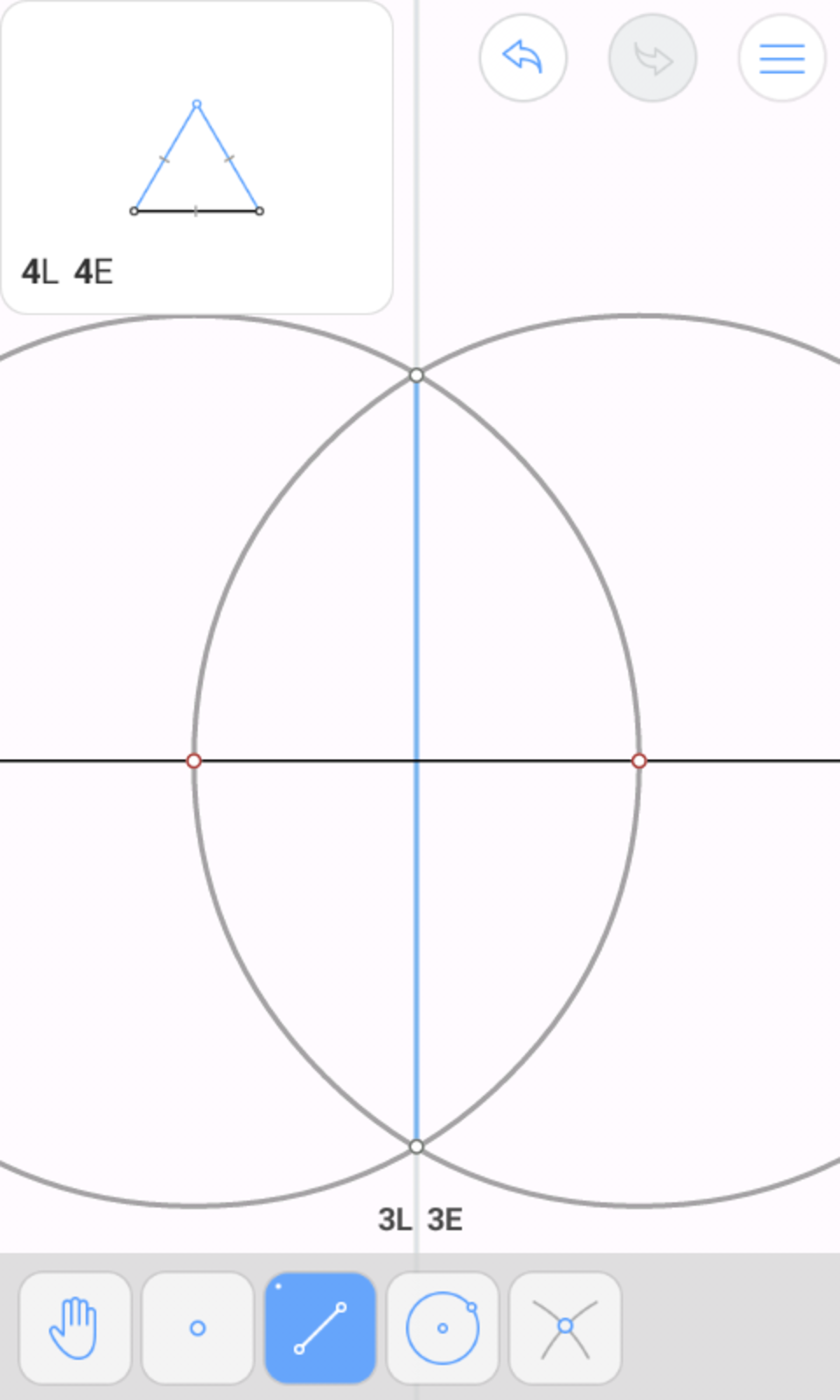
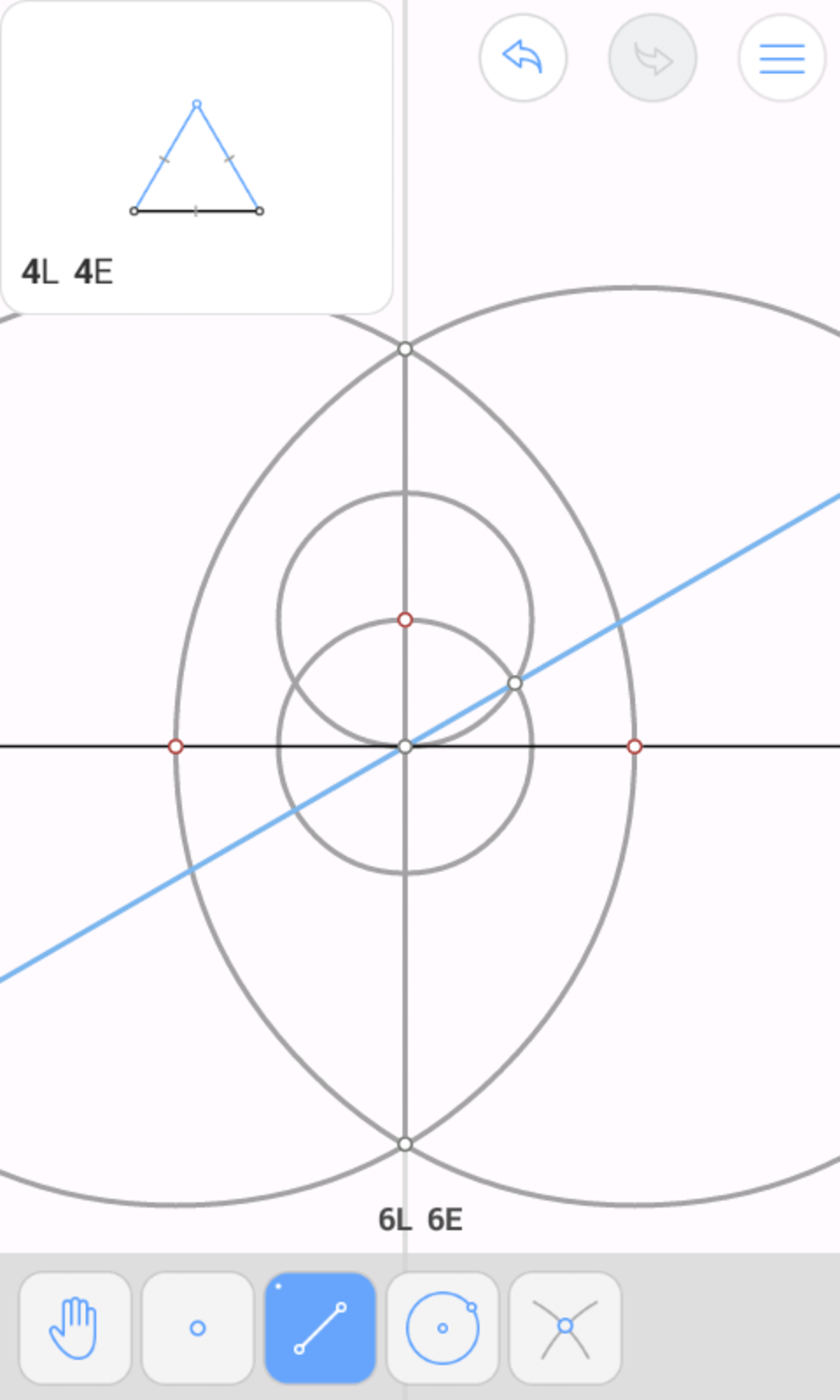
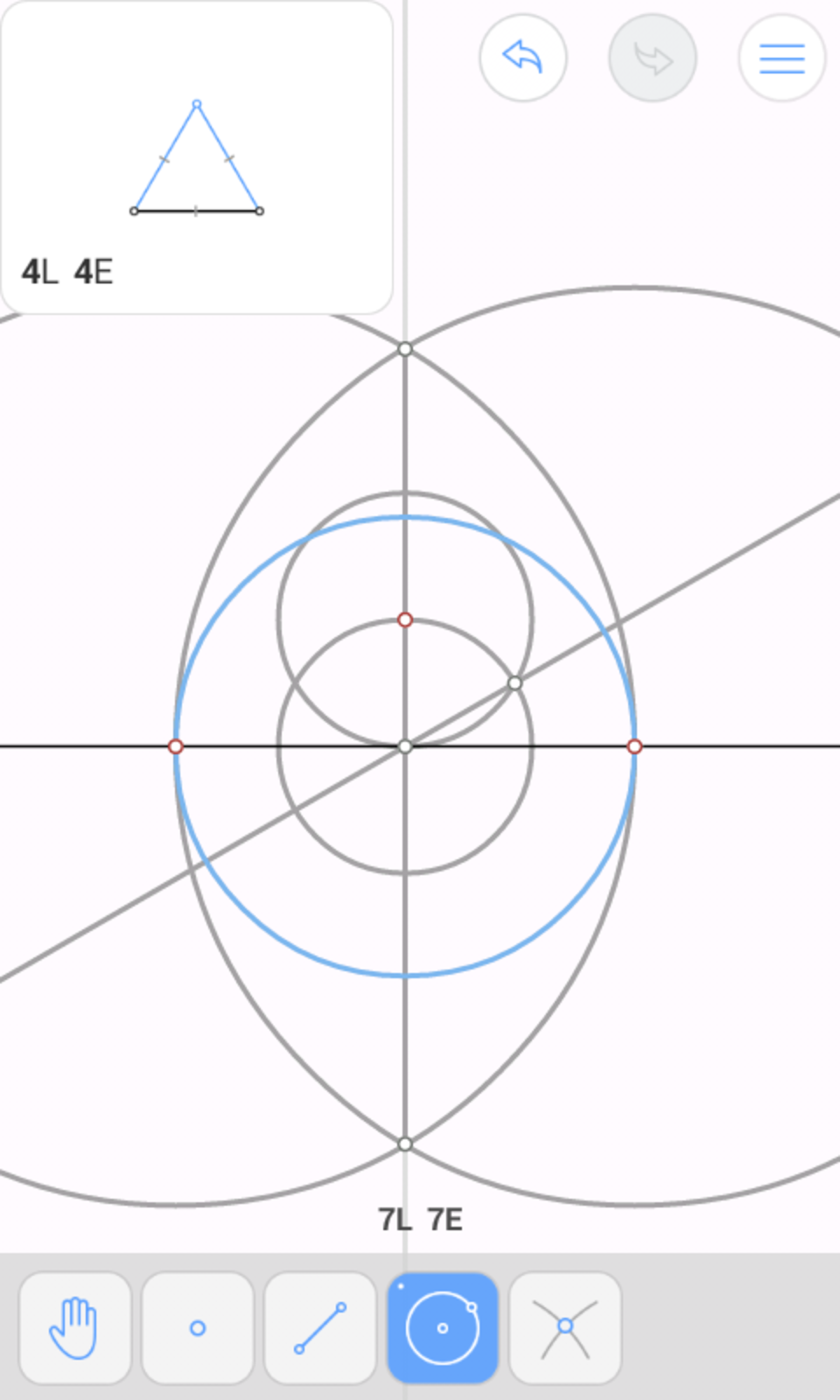
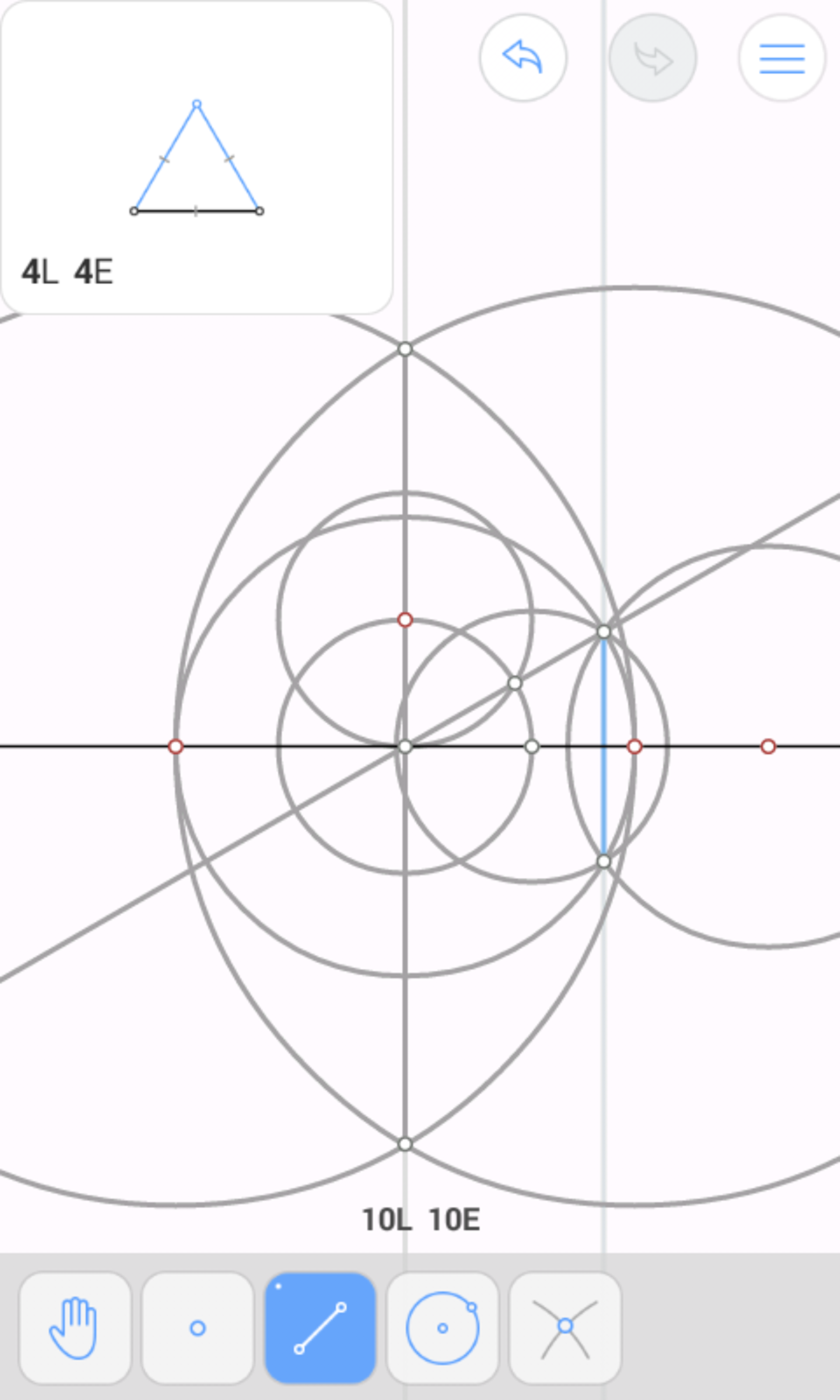
Since $(2 - \sqrt{3}) : (2 + \sqrt{3}) = 1 : (7 + 4\sqrt{3})$ , we're looking to construct $\frac{1}{1 + (7 + 4\sqrt{3})} = \frac{1}{8 + 4\sqrt{3}} = \frac{1}{4} (2 - \sqrt{3})$ of a line segment. Since this is a constructible number, the answer is yes .

One example construction: Call our line segment $AB$ .

1. Construct the midpoint of $AB$ , call it $C$ . (Standard construction: circle with center $A$ and radius $AB$ and circle with center $B$ and radius $BA$ intersect at two points $X, Y$ ; $XY$ and $AB$ intersect at the desired $C$ .)
2. Construct the midpoint of $AC$ , call it $D$ . (Same construction.)
3. Draw a perpendicular of $DA$ at $D$ , call it $l_1$ . (Standard construction: circle with center $D$ and radius $DA$ intersects $AD$ at a point $Z$ (which happens to be $C$ , but we'll generalize); now construct midpoint of $AZ$ with the above standard construction, we will get the line $XY$ that intersects $AZ$ at $D$ . This time, we take $XY$ instead; it's the perpendicular.)
4. Circle with center $D$ and radius $DA$ intersects $l_1$ at two points $E, E'$ .
5. Circle with center $C$ and radius $CE$ intersects the interior of $AC$ at a point $F$ .
6. Draw a perpendicular of $FA$ at $F$ , call it $l_2$ .
7. Draw a perpendicular of $ED$ and $E$ , call it $l_3$ .
8. $l_2$ and $l_3$ intersect at $G$ .
9. Circle with center $C$ and radius $CG$ intersects the interior of $AC$ at a point $H$ .
10. Now $AH : HB = (2 - \sqrt{3}) : (2 + \sqrt{3})$ .

Proving it is easy. Treat $AB$ as having 4 units length. Then $AD = DC = \frac{1}{4} AB = 1$ . Also, $DE = DA = 1$ , so $CE = CF = \sqrt{2}$ . Since $AB$ is perpendicular to both $DE$ and $FG$ , the latter two are parallel. Since $AB$ is parallel to $EG$ , $DEGF$ is a rectangle, so $FG = DE = 1$ . Thus $CG = CH = \sqrt{3}$ . So $AH = 2 - \sqrt{3}$ , and by subtraction, $HB = AB - AH = 2 + \sqrt{3}$ .