Maybe that's too much work
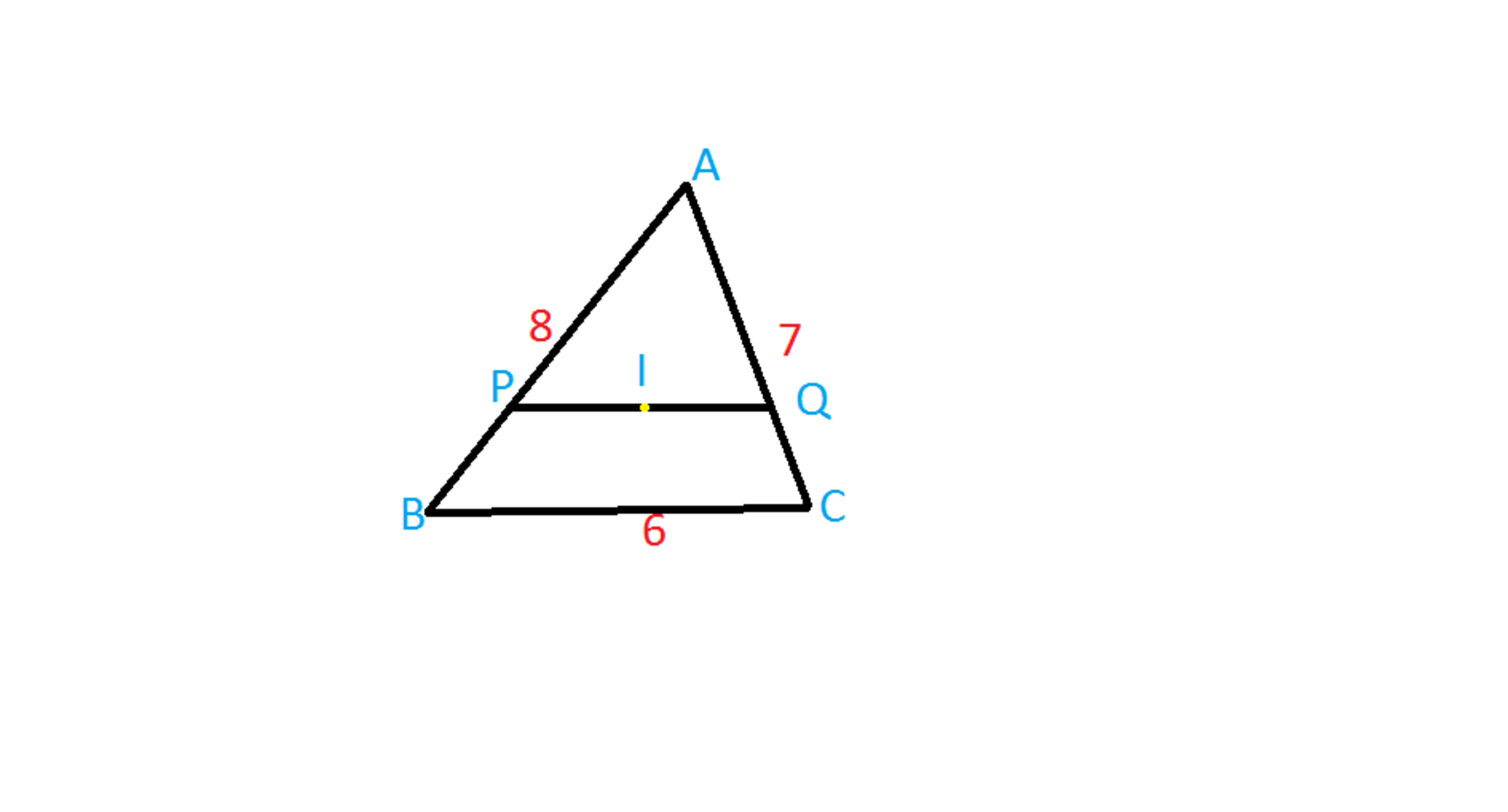
A triangle ABC has sides 6 ,7 , 8 units . The line through its incentre parallel to the shortest side is drawn to meet the two other sides at P and Q.
Find the length of the line segment PQ ; it is of the form z a .
-
Evaluate a z and express it in base z . Let's name it as k .
- Now find it's a t h root taking k in base 10 .
-
Report the least integer greater than it .
You can try more of my Questions here .
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Azhaghu Roopesh M Thanks for making the changes; it's quite clear now what you are asking for. :)
Did exactly the same! Nice question!
My solution was similar to Brian's up to the point of the triangle similarity. I worked it like this:
Firstly, I will find the radius of the incircle. I will do this by finding the area S of the triangle:
Let s be the semiperimeter of the triangle. Then, s = 2 2 1 . Thus:
S = 2 2 1 2 5 2 7 2 9 = 4 2 1 1 5
Now, the radius r can be found using the formula: S = s ∗ r
Therefore, r ∗ 2 2 1 = 4 2 1 1 5 → r = 2 1 5 .
Now, we find the distance from the opposite vertex to the smallest side. This can be done by using areas once more: 2 6 ∗ d = 4 2 1 1 5
Thus, d = 4 7 1 5
Now, using triangle similarity, let P Q = x . Then: x d − r = 6 d .
x 4 5 1 5 = 6 4 7 1 5
x 5 = 6 7
x = 7 3 0
Now, a z = 3 0 7 in base 1 0 ; 3 0 1 0 = 4 2 7 , and then in base 7 we have a z = 1 4 0 2 6 4 6 6 3 4 6 4 2 7
The 3 0 -th root of the number 1 4 0 2 6 4 6 6 3 4 6 4 2 1 0 is approximately 2 . 5 4 , and thus the number sought is 3.
The formula for the radius r of the incenter is r = s A , where A is the area of the triangle and s is the semi-perimeter.
Using Heron's formula A = s ( s − a ) ( s − b ) ( s − c ) where a , b , c are the side lengths, we find that
A = ( 2 2 1 ) ( 2 9 ) ( 2 7 ) ( 2 5 ) = 4 2 1 1 5 .
Thus r = 2 2 1 4 2 1 1 5 = 2 1 5 .
Now draw an altitude from A to B C . Let this altitude intersect P Q at M and B C at N . Then
B C P Q = A N A M ⟹ P Q = 6 A N ( A N − r ) .
So now we need to find A N . The Cosine rule gives us that
7 2 = 6 2 + 8 2 − 2 ( 6 ) ( 8 ) cos ( ∠ B ) ⟹ cos ( ∠ B ) = 9 6 5 1 = 3 2 1 7
sin ( ∠ B ) = 1 − ( 3 2 1 7 ) 2 = 3 2 7 1 5 .
Thus A N = 8 sin ( ∠ B ) = 4 7 1 5 , and so
P Q = 6 4 7 1 5 4 7 1 5 − 2 1 5 = 7 3 0 .
So now we need to find the 3 0 th root of 3 0 7 as expressed in base 7 . Using WolframAlpha we have that 3 0 7 in base 7 is 1 4 0 2 6 4 6 6 3 4 6 4 2 , the 3 0 th root of which is 2 . 5 4 0 3 7 7 6 . . . . , the least integer greater than this being 3 .
(I assumed that the 3 0 th root was to be taken as if 3 0 7 in base 7 was a base 1 0 number. I found the wording a bit confusing. @Azhaghu Roopesh M Is this what you had in mind once the value P Q = 7 3 0 was found?)