Measuring perimeters

Geometry Level 2

In the diagram, the left side of the square is tangent to the circle and two vertices of the square are lying on the circle.

Which has a larger perimeter, the square or the circle?

The square The circle They have equal perimeters

4 solutions

Uros Stojkovic
Jul 5, 2017

$p^{2}=a^{2}+\frac{a^{2}}{4}$ , $q^{2}=\frac{a^{2}}{4}+(2r-a)^{2}$

$\begin{aligned} 4r^{2} & =p^{2}+q^{2} \\ &=a^{2}+\frac{a^{2}}{4}+\frac{a^{2}}{4}+4r^{2}-4ar+a^{2}\end{aligned}$

$0=2a^{2}+\frac{a^{2}}{2}-4ar$

$\begin{aligned} 5a^{2} & =8ar \\ & \Rightarrow 5a=8r \\ & \Rightarrow a=\frac{8}{5}r \end{aligned}$

$P=4\times \frac{8}{5}r= 6,4r$

$C=2r\pi \approx 6,28r$ .

Hence, $\boxed{P> C}$ .

Ronald Chén
Jul 6, 2017

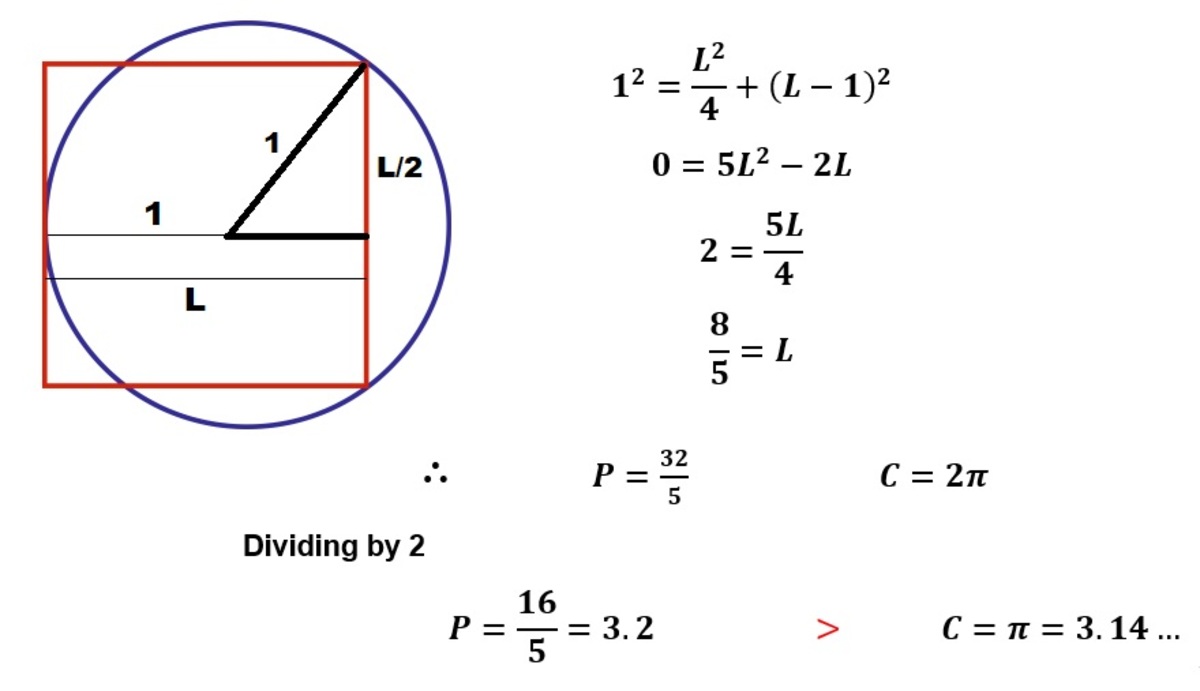
Question: Will there be a solution where it is not necessary to know the value of π. That is, a purely geometric solution, which only explores the relation between the square and the circumference?

Is using the Archimedean method to find pi cheating? Just show the outer polygon perimeter converges to a value less than 6.4r. If it is

Use the rectangular curve length formula to calculate the circumference (parametric and polar versions require $\pi$ from the very start) Let the circle center be the origin. There's a factor of two because the integral by itself only gives us half the circumference.

$6.4r>2\int_{-r}^{r}\sqrt{1+\left ( \frac{dy}{dx} \right )^2} dx$
$6.4r>2\int_{-r}^{r}\sqrt{1+\left ( \frac{-x}{\sqrt{r^2-x^2}} \right )^2} dx$
$6.4r>2r\int_{-r}^{r}\sqrt{\frac{r^2}{r^2-x^2}} dx$

Let r=1

$3.2>\int_{-1}^{1}\sqrt{\frac{1}{1-x^2}} dx$

Plotting the integrand as a function of x on the graph and you'll see the area between its boundaries x=-1 and x=1 will be smaller than a rectangle 2 units wide and 3.2 units high.

Jack Han - 3 years, 11 months ago

Interesting! I think I would not have thought of a solution this way.

Ronald Chén - 3 years, 10 months ago

Jack Han
Jul 16, 2017

What we know:

Let center of circle be origin $(0,0)$
Top right vertex: $(r\cos(a),r\sin(a))$
Bottom right vertex $(r\cos(-a),r\sin(-a))=(r\cos(a),-r\sin(a))$
Top left vertex: $(-r,rsin(a))$
Bottom left vertex $(-r,r\sin(-a))=(-r,-r\sin(a))$
$0\leq a\leq \frac{\pi}{2}$

From this:

Top and bottom edges have length $r+r\cos(a)$
Left and right edges have length $2r\sin(a)$
These must be equal because the shape is a square: $l=r+r\cos(a)=2r\sin(a)$

Solving for $a$ , the general solution is $a=2(\pi n+\arctan(\frac{1}{2}))$ where $n \in \mathbb{Z}$ . The only $a$ that satisfies this and the constraint $0\leq a\leq \frac{\pi}{2}$ is when $n=0$

$a=2\arctan(\frac{1}{2})$

Plug this into $l=r+r\cos(a)=2r\sin(a)$ and we get $l=1.6r$ The perimeter of the square is therefore $6.4r$

Meanwhile, the perimeter of the circle is $2\pi r \approx 6.3r$ ,

Therefore the square has the larger perimeter.

Auro Light
Jul 16, 2017

Let the square be ABCD, and the side AB intersecting circle at P.
According to tangent-secant theorem,
(Tangent)^2 = (whole secant)×(external secant).
(AD/2)^2 = (AB)×(AP), since AD=AB,
We have, AP = AB/4.
Let side length of square be AB = 4a,
We have, AP=a, PB=3a and BC=4a,.
So, by Pythagoras theorem,.
PC^2 = PB^2 + BC^2 = 9a^2+16a^2=25a^2,.
PC = 5a. Now, PC has to be diameter of the circle because angle PBC = 90°.
So, radius = PC/2 = 5a/2.
Perimeter of square =4×4a = 16a,
And circumference of circle = 2π(5a/2) = 5πa,.
Since 16a > 5πa, perimeter of square is bigger.

Measuring perimeters

4 solutions

0 pending reports