Mechanical Movement
A pink ball is connected to a blue ball by a straight, 15-meter metal rod. The blue ball moves horizontally on the -axis at a constant speed of while the pink ball moves vertically on the -axis. So, as shown, when the blue ball moves left and right between and the point the pink ball rises and falls peaking at the point
To 3 significant figures, what is the absolute speed of the pink ball (in meters per second) when the blue ball is at
The answer is 0.354.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Call the distance of the blue ball from the centre 'B', and the distance of the pink ball from the centre 'P'.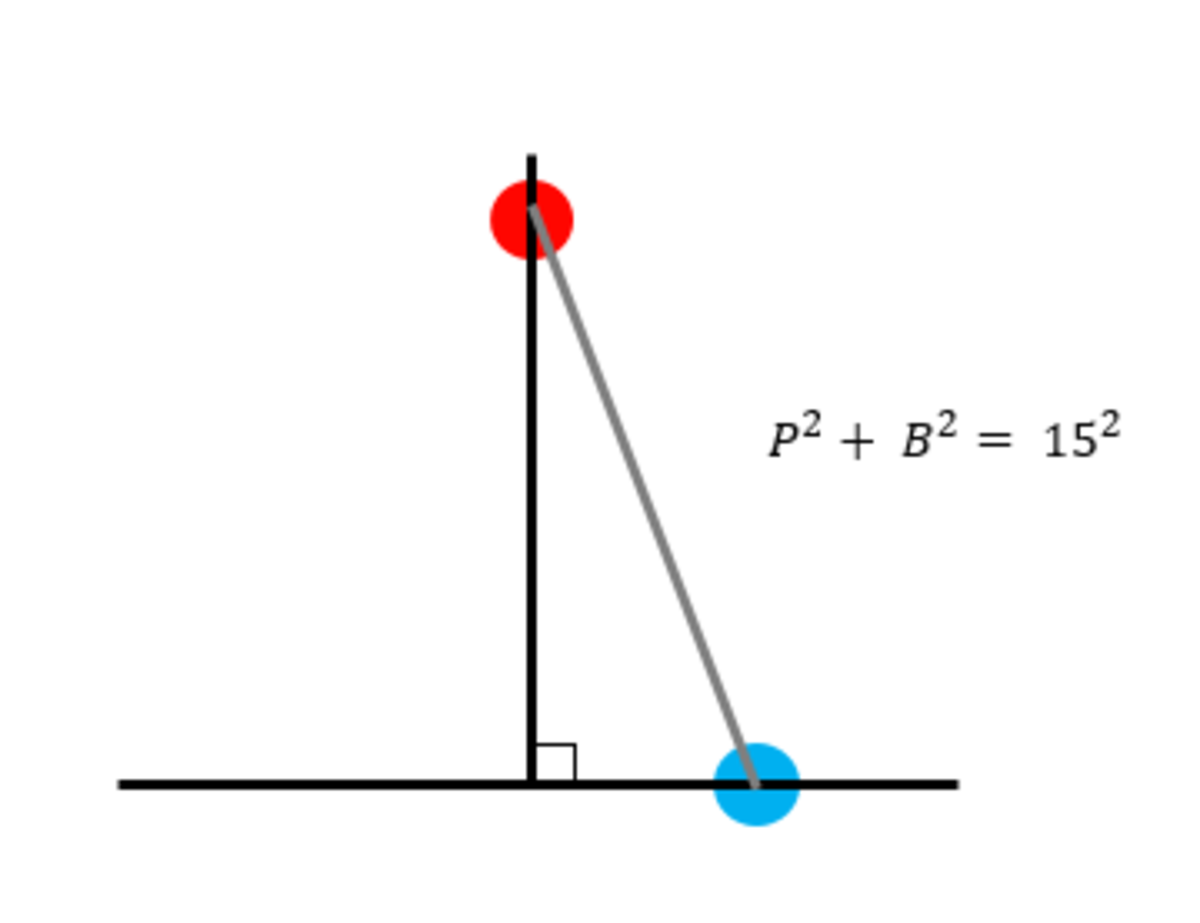
The way I did this was to plot the movement of the blue ball on a distance-time graph:
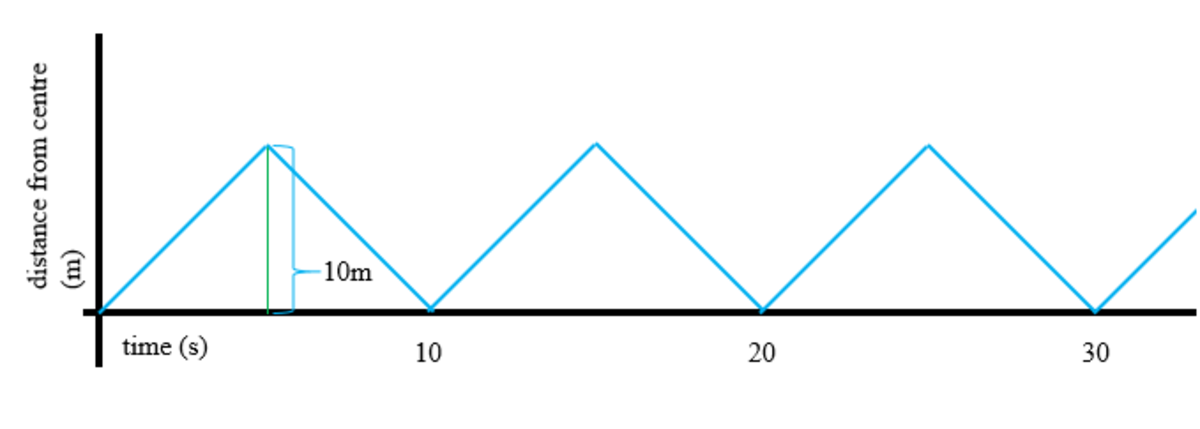As we can see, the distance of the blue ball from the centre increases and decreases at a constant rate.
However, for the motion of the pink ball, note that
P
2
+
B
2
=
1
5
2
is the equation for a
circle
. This means that the graph for the pink ball looks something like this:
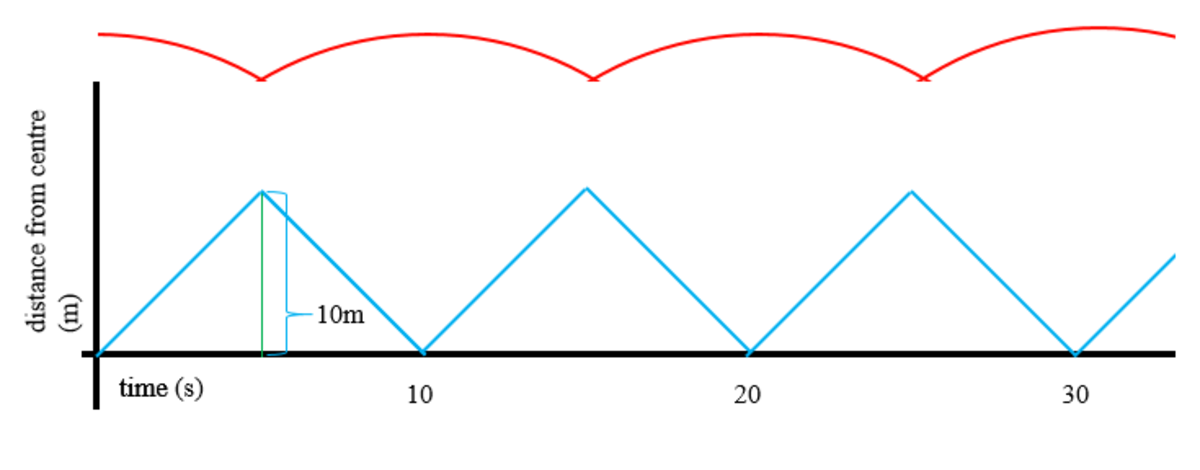The graph for the pink ball is a series of arcs that are formed by overlapping circles.
Since this is a distance-time graph, working out the gradient of the pink graph at the correct point will give us the correct speed. Since the pink graph is composed of circles, we can do this by working out the gradient of the radius to the relative point, then the gradient of the tangent. The method is in the image below.
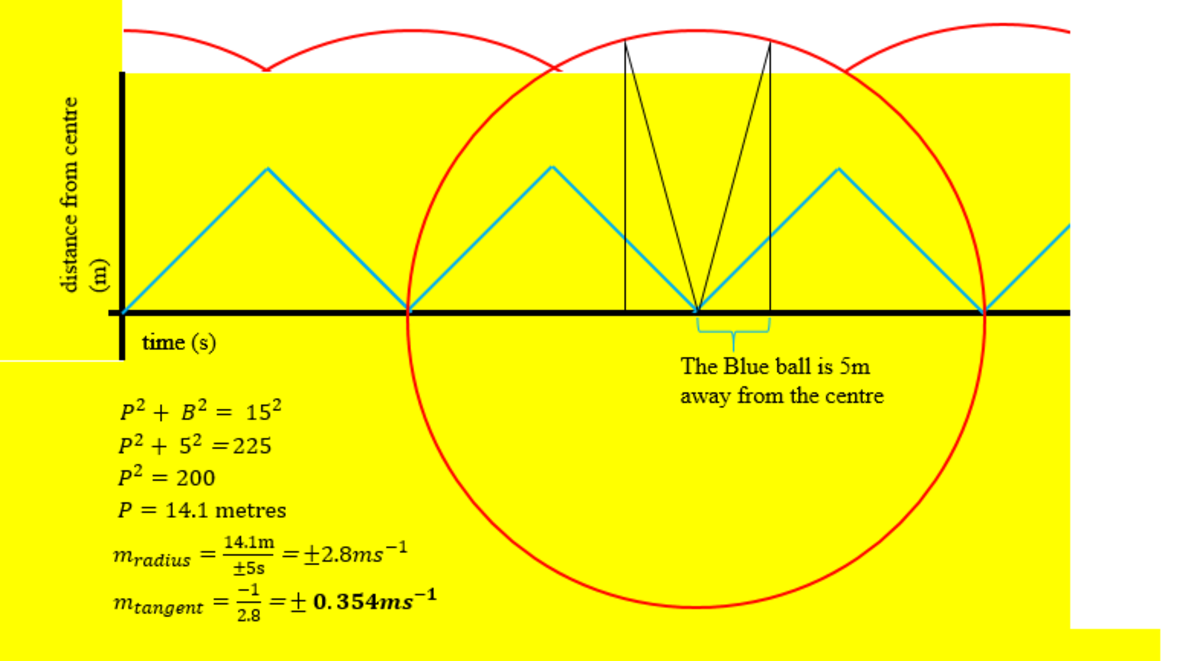Therefore, the speed of the pink ball when the blue ball is halfway is
0
.
3
5
4
m
s
−
1
At the time of editing this solution, I realise that the answer to problem is currently incorrect. I apologise for this, and I hope that Brilliant can change it to the correct answer soon.