Mechanics |10-06-2021|
A particle of mass
is connected with the fixed vertical cylinder with the help of a string of length
as shown in the figure .The particle is given a horizontal velocity
perpendicular to the string and it moves on the smooth horizontal surface .
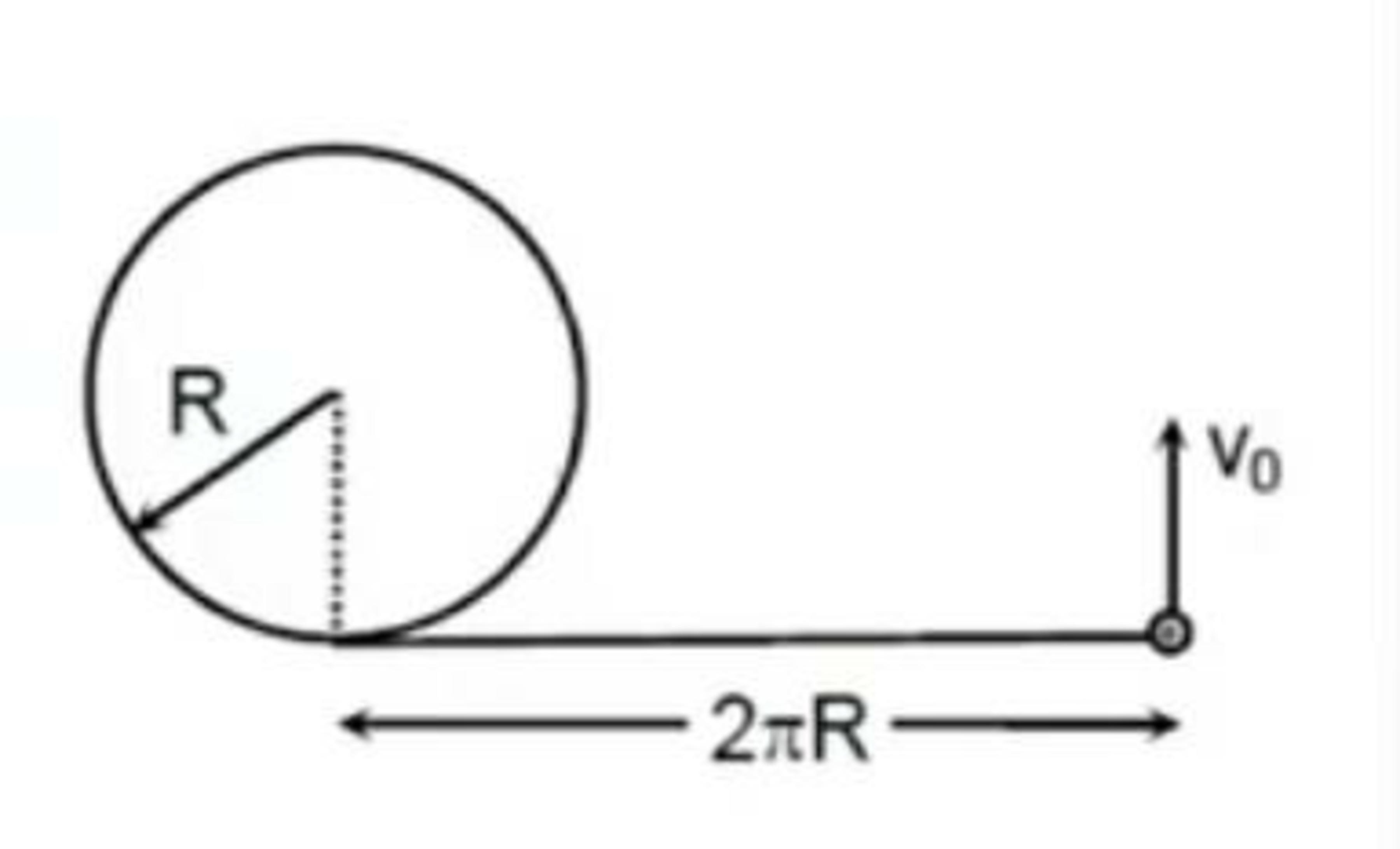
A
= Speed of particle increases continuously.
B
= Speed of particle remains constant.
C
= Tension in the string increases continuously.
D
= Time after which the particle will collide with the cylinder is
.
.
The option/s which are correct ,Type the answer as sum of the square of their values .
The answer is 29.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the center of the cylinder cross section be the origin of the coordinate frame. After rolling the string by an angle θ about the circumference of the cylinder, a length of R θ will be wound about the cylinder, and therefore the coordinate of the particle will be
p = R ( sin θ , − cos θ ) + ( 2 π R − R θ ) ( cos θ , sin θ )
Taking the time-derivative of this expression,
p ˙ = R ( cos θ , sin θ ) θ ˙ + ( − R θ ˙ ) ( cos θ , sin θ ) + ( 2 π R − R θ ) ( − sin θ , cos θ ) θ ˙
which simplifies to,
p ˙ = ( 2 π R − R θ ) θ ˙ ( − sin θ , cos θ )
Since ( − sin θ , cos θ ) is a unit vector, the speed of the particle is given by
v = R ( 2 π − θ ) θ ˙
We can now apply the Lagrangian equation method, where since the motion is in the horizontal plane, the potential V is zero, and L = T , that is,
L = 2 1 m v 2 = 2 1 m R 2 ( 2 π − θ ) 2 ( θ ˙ ) 2 = 2 1 m R 2 ( 2 π − θ ) 2 ω 2
where ω = θ ˙ .
The equation of motion is derived from
d t d ( ∂ ω ∂ L ) = ∂ θ ∂ L
and this evaluates to,
2 1 m R 2 d t d ( 2 ω ( 2 π − θ ) 2 ) = 2 1 m R 2 ω 2 ⋅ ( − 2 ) ( 2 π − θ )
Cancelling m R 2 on both sides, and evaluating the time derivative on the left side, this becomes,
ω ˙ ( 2 π − θ ) 2 − 2 ω 2 ( 2 π − θ ) = − ω 2 ( 2 π − θ )
Dividing by ( 2 π − θ ) and simplifying,
ω ˙ ( 2 π − θ ) = ω 2
If we let u = ( 2 π − θ ) , then u ˙ = − ω , and u ¨ = − ω ˙ , hence,
u ¨ u + u ˙ = 0
That is to say,
d t d ( u u ˙ ) = 0
Which implies that
u u ˙ = K , where K is a constant.
Plugging in the expression for u and u ˙ , gives us,
( 2 π − θ ) ( − θ ˙ ) = K
From this equation we deduce that the speed of the particle remains constant, and that constant is ( − R K ) . This is expected because the motion is in the horizontal plane, and the potential energy of the particle remains constant, so its kinetic energy remains constant as well (since the total energy is conserved).
From u u ˙ = K , by separating the variables, and integrating, we get
u 2 − u ( 0 ) 2 = 2 K t
Thus
( 2 π − θ ) 2 − ( 2 π ) 2 = − 2 v 0 / R t
At the final instant, we have θ f = 2 π , and hence,
t f = v 0 2 π 2 R
Thus option A is false, while options B and D are true. What remains is option C which is a statement about the tension in the string , by taking the derivative of p ˙ , we get,
p ˙ = ( 2 π R − R θ ) θ ˙ ( − sin θ , cos θ )
p ¨ = R [ ( − ω 2 + ( 2 π − θ ) ω ˙ ) ( − sin θ , cos θ ) + ( 2 π − θ ) ω 2 ( − cos θ , − sin θ ) ]
This is the expression for the acceleration of the particle and it is proportional to the tension in the string.
The first term is identically zero, from the analysis above, therefore,
p ¨ = R ( 2 π − θ ) ω 2 ( − cos θ , − sin θ )
Since ( − cos θ , − sin θ ) is a unit vector, the magnitude of acceleration is
a = R ( 2 π − θ ) ω 2
Also, from the above analysis, we have,
θ = 2 π − 4 π 2 − 2 ( v 0 / R ) t
Thus,
ω = 4 π 2 − 2 ( v 0 / R ) t ( v 0 / R )
Hence, the acceleration magnitude is
a = R 4 π 2 − 2 ( v 0 / R ) t ( 4 π 2 − 2 ( v 0 / R ) t ) ( v 0 / R ) 2 = 4 π 2 − 2 ( v 0 / R ) t ( v 0 2 / R )
As the time t progresses, the denominator decreases, and therefore, a increases, therefore the force acting on the particle (which is the tension in the string) must be increasing.
Thus choice C is also true.
This makes the answer ( 2 ) 2 + ( 3 ) 2 + ( 4 ) 2 = 4 + 9 + 1 6 = 2 9