Mechanics - 12

Classical Mechanics Level 3

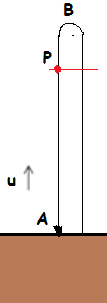The gap shown is just for sake of understanding The gap shown is just for sake of understanding A stone which is at a A A is projected vertically upwards. It passes through a fixed point P P , two seconds after its projection. After three more seconds it again passes through P P but this time it is falling towards ground. What is the speed of the projection of the stone (in m/s \text{m/s} ) ?

Assume g = 9.8 m/s 2 g = \text{9.8 m/s}^2

Try my World of Physics to solve many problems like this one.


The answer is 34.3.

Ram Mohith by Ram Mohith , 18, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

The height h h of the projectile time t t after projection with an initial velocity u u is given by: h = u r − 1 2 g t 2 h = ur - \dfrac 12 gt^2 . If point P P is h h above the ground then

{ h = 2 u − 2 g . . . ( 1 ) h = 5 u − 12.5 g . . . ( 2 ) \begin{cases} h = 2u - 2 g & ...(1) \\ h = 5u - 12.5g & ...(2) \end{cases}

( 2 ) − ( 1 ) : 3 u − 10.5 g = 0 ⟹ u = 10.5 3 g = 10.5 3 × 9.8 = 34.3 m/s \begin{aligned} (2) - (1): \quad 3u - 10.5 g & = 0 \\ \implies u & = \frac {10.5}3 g = \frac {10.5}3 \times 9.8 = \boxed{34.3} \text{ m/s} \end{aligned}

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...