Breaking Rod

Relevant Wiki : rotational kinetic energy - conservation of energy

The first part of the problem says that the rod is released from horizontal position and rotates in vertical plane by an angle $90^{\circ}$ . Let the angular velocity of rod about the hinge be $\omega$ . Firstly lets find out the angular velocity of the rod: Applying conservation of energy, $\begin{aligned} \frac{mgl}{2} &= \frac{1}{2} I \omega ^2 \\ I= \frac{ml^2}{3} \\ \Rightarrow \omega &= \sqrt{\frac{3g}{l}} & (1) \\ \end{aligned}$ Now the question says that as soon as the rod becomes vertical it breaks from its midpoint and there is no effect on the motion of any part of rod during the process of separation. So now we consider the lower part of the rod as a separate body and study its motion. 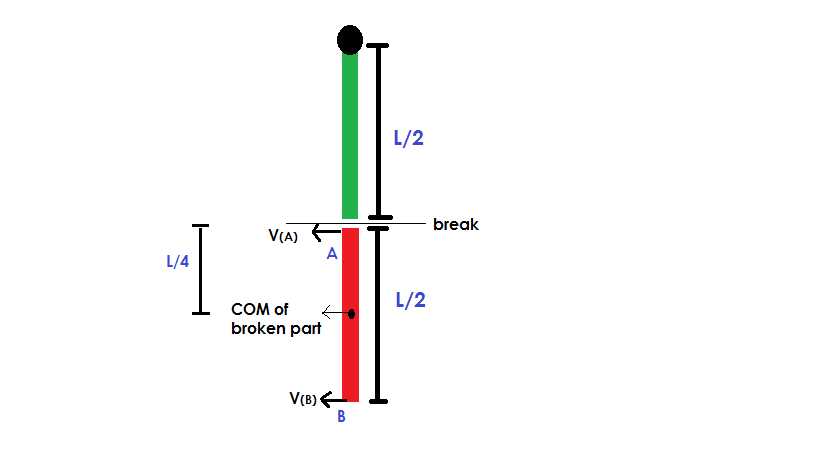The center of mass of the lower rod is at a distance of $\frac{3l}{4}$ from the hinge. Let $\omega _0$ be the angular velocity of the rod about its new centre of mass. We can write velocity of center of mass of lower rod as : $\begin{aligned} v_{com} &=\omega \times \frac{3l}{4} \\ \omega_0 &= \frac{v_B - v_A}{AB} \\\\ v_A= \frac{\omega l}{2} && v_B =\omega l \\ & AB=\frac{l}{2} \\\\ \Rightarrow \omega_0 & = \omega & (2) \\ \end{aligned}$ The motion of lower rod after separation will be combination of translation motion and rotation motion about its center of mass. The angular velocity of the lower rod will remain unchanged during subsequent motion because no torque acts on it (The weight of the rod acts about it center of mass and hence passes through the axis of rotation and hence produces no torque). The lower rod will become vertical again after it rotates by an angle $180^{\circ}$ about its axis (passing through center of mass and perpendicular to the rod). Hence time taken by rod to rotate by $180^{\circ}$ is:
$\begin{aligned} t &= \frac{\pi}{ \omega_0} \\ \end{aligned}$ Using equation of motion we calculate the horizontal and vertical displacement of the com of lower rod : $\begin{aligned} y &= \frac{1}{2}gt^2 \\ x &= v_{com} t \end{aligned}$ Hence distance of the center of lower rod from the hinge (d) is given by: $\begin{aligned} d &= \sqrt{ x^2 + (y+\frac{3l}{4})^2} \\ \end{aligned}$ Substituting the values of given variables in SI units, you get: $\begin{aligned} \omega &= \SI{6.324}{\radian\per\second} \\ v_{com} &= \SI{3.557}{\meter\per\second} \\ t &= \SI{0.496}{\second} \\ x &= \SI{1.767}{\meter} \\ y &= \SI{1.233}{\meter} \\\\ \large{d} &=\boxed{\SI[per-mode=symbol]{2.519}{\meter}} \end{aligned}$

Hints :

• For a body doing rotation (or combined motion ) - the angular velocity of body about any point is the same .
• Since it detaches smoothly , no change in velocity of any part!