Mechanics + Magnetism = Mechatism 3
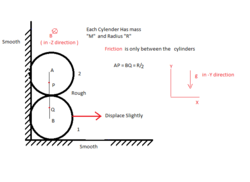 As shown in figure there is Two Identical Conducting Hollow Cylinders each of mass M and Radius R . And there is sufficiently Friction between two the cylinders only.
As shown in figure there is Two Identical Conducting Hollow Cylinders each of mass M and Radius R . And there is sufficiently Friction between two the cylinders only.
Now If Lower cylinder is displace slightly to the rightward direction .And If Maximum velocity of lower cylinder is .
Assume that whole system is placed in uniform magnetic field of strength B . which is perpendicular to the plane of cylinders ( - Z direction )
And If Magnitude of Motional EMF develop between the point P and Q just before the lower cylinder reaches it's maximum velocity is .
Then Find The value of .
This is part of set Mixing of concepts
Try This first Click here
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
I upload full solution later but you can see this question solution and also This Note
This question is combination of these two question's.
Update For calculating maximum velocity :
Here is my method when friction is present between only cylinders. By using concept of Instantaneous centre of rotation [ ICR ]
Because This system is an equivalent Rigid Body. Since There is no relative motion between point of contact of cylinder.
The whole system is assumed to be purely rotated about "O"
Then
so velocity of any point P of this combined system in ICR ( O ) frame is given By
V p / o = r p / 0 × ω 0 .
V 1 = ( 2 R cos θ ) ω 0 V 2 = ( 2 R sin θ ) ω 0 ⇒ ω 0 = 2 R V 1 2 + V 2 2 .
Now using energy conservation of system in ICR frame we get
2 g R ( 1 − cos θ ) = 2 1 I o ω 0 2 ⟶ ( 1 ) I o = m R 2 + m R 2 + 4 m R 2 cos 2 θ + 4 m R 2 sin 2 θ I o = 6 m R 2 ⇒ ω 0 = 3 R 2 g ( 1 − cos θ ) ⟶ ( 2 ) V 1 2 = 3 8 g R ( 1 − cos θ ) cos 2 θ ⟶ ( 3 ) V 2 2 = 3 8 g R ( 1 − cos θ ) sin 2 θ ⟶ ( 4 ) .
Now using maxima concept on velocity of cylinder - 1 ( Lower Cylinder )
d θ d ( V 1 2 ) = 0 θ = cos − 1 3 2 O r θ = 0 × ( r e j e c c t e d ) O r θ = 2 π × ( r e j e c t e d ) .
So again cylinder will loose contact at the same hight as that of in 1st Part of this question ( when no friction ) I rejected other values of angle because velocity of lower cylinder never be zero. And Now Further Motion is independent
So we get maximum velocity of lower block
V 1 , m a x = 8 1 3 2 g R .
Now for Calculating Motional emf See similiar type This Question Solution Mechatism 2