Mechanics or what?

Electricity and Magnetism Level 2

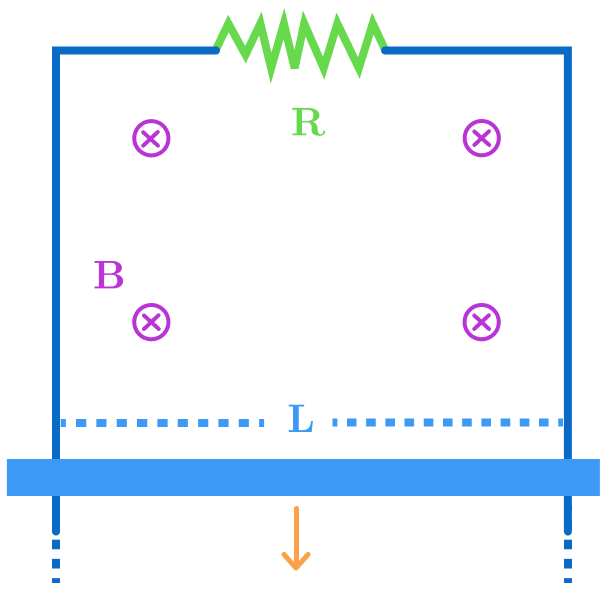
A horizontal conducting rod of mass m m is free to slide on two vertical conducting rails as shown. What is the terminal speed of the rod?

Details and Assumptions:

  • A uniform magnetic field of intensity B B exists throughout the region and points into the screen.
  • The length of the rod is L L .
  • The resistor has resistance R R .

Bonus What will happen if the magnetic field is outward? Will the rod attain terminal velocity?

Try my next problem here

m g L B R \dfrac{mgL}{BR} B 2 L 2 m g R \dfrac{B^2L^2}{mgR} m g R B 2 L 2 \dfrac{mgR}{B^2L^2} m g R B L \dfrac{mgR}{BL}

Sparsh Sarode by Sparsh Sarode , 22, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Sparsh Sarode
Jun 23, 2016

At terminal velocity, induced EMF, e = B v L e=BvL where v is the terminal velocity of the rod

i = e R i=\dfrac{e}{R}

i = B v L R i=\dfrac{BvL}{R}

Upwards force experienced by rod is

F B = B i L F_B=BiL

F B = B 2 L 2 v R F_B=\dfrac{B^2L^2v}{R}

This should be equal to m g mg

∴ v = m g R B 2 L 2 \therefore v=\dfrac{mgR}{B^2L^2}

6 Helpful 0 Interesting 0 Brilliant 0 Confused

Not as easy as it looks!!!

Rishi K - 4 years, 11 months ago

Log in to reply

Yep. What about the bonus question?

Sparsh Sarode - 4 years, 11 months ago

Log in to reply

Thats brilliant too...:p

Rishi K - 4 years, 11 months ago

Actually, if you look really closely at the options, dimensional homogeneity can be used, though that method is a little bland. This answer is much more satisfying!

B.S.Bharath Sai Guhan - 4 years, 11 months ago

I also did this by dimensional method . Its quite easy.but this is a more vivid soln.

Sargam yadav - 4 years, 11 months ago

is there a good wiki to look at for this?

Matthew Agona - 4 years, 6 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...