Mechanism of Mechanics.
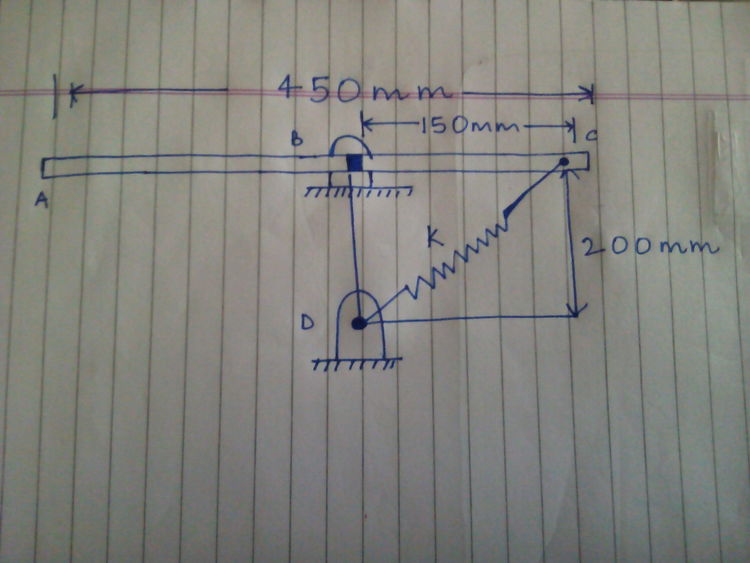 A
Kg uniform rod rotates in a vertical plane about a smooth pivot at
. A spring of constant
N/m and of unstretched length
mm is attached to The rod as shown .Knowing that in the position shown the rod has an angular velocity of
rad/s clockwise,determine the angular velocity of The rod after it has rotated through
.
A
Kg uniform rod rotates in a vertical plane about a smooth pivot at
. A spring of constant
N/m and of unstretched length
mm is attached to The rod as shown .Knowing that in the position shown the rod has an angular velocity of
rad/s clockwise,determine the angular velocity of The rod after it has rotated through
.
Take m/s^2
The answer is 6.182.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Use conservation of energy: Δ K + Δ U g + Δ U s = 0 . First, for the kinetic energy term, consider the rotation of the rod about its CM and the motion of the CM. The CM is located d = 4 5 0 / 2 − 1 5 0 = 7 5 mm to the left of the pivot. K = K r o t + K t r = 2 1 I ω 2 + 2 1 m v C M 2 = 2 1 m ( 1 2 1 ℓ 2 + 2 1 d 2 ) ω 2 = 0 . 0 3 3 7 5 ω 2 ; The gravitational potential energy increases because the CM is raised vertically over a distance d : Δ U g = m g d = 2 . 2 5 J . The spring was first stretched and ends up compressed. In the initial situation, the length of the spring is 1 5 0 2 + 2 0 0 2 = 2 5 0 mm; in the final situation, 2 0 0 − 1 5 0 = 5 0 mm. Thus Δ U s = 2 1 k Δ u 2 = 1 5 0 ( ( 5 0 − 1 0 0 ) 2 − ( 2 5 0 − 1 0 0 ) 2 ) = − 3 . 0 0 J . Thus we have 0 . 0 3 3 7 5 ( ω ′ 2 − ω 0 2 ) + 2 . 2 5 − 3 . 0 0 = 0 , ω ′ 2 = ω 0 2 + 0 . 0 3 3 7 5 0 . 7 5 , ω ′ = 4 2 + 2 2 . 2 2 2 = 6 . 1 8 2 4 1 rad/s .