Medals Are For Stars
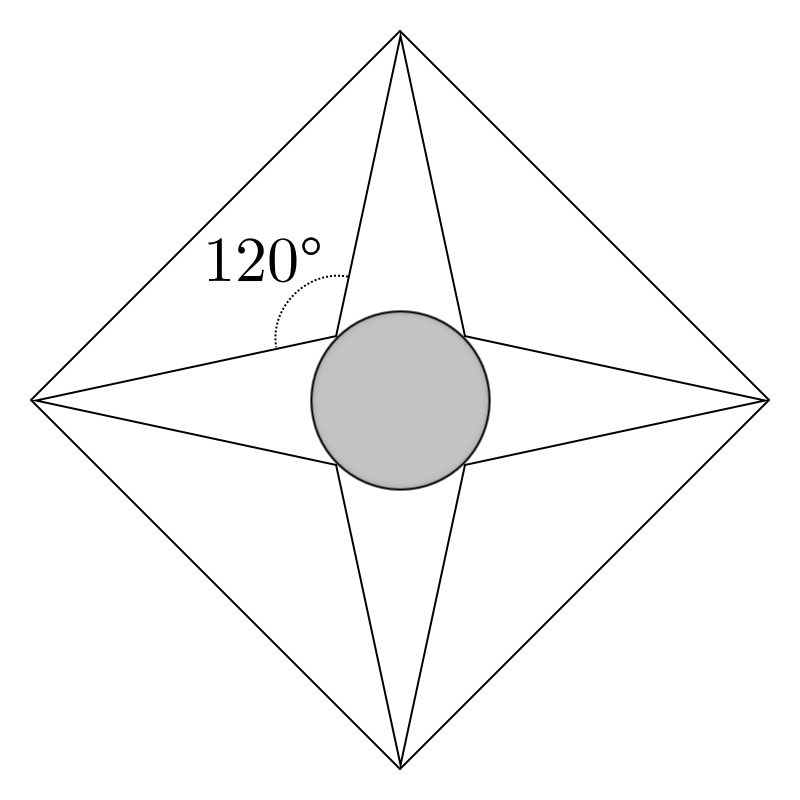 A medal is formed by incsribing a four-pointed star in a diamond of side 1, such that the angle between the points is
1
2
0
∘
as shown.
A medal is formed by incsribing a four-pointed star in a diamond of side 1, such that the angle between the points is
1
2
0
∘
as shown.
If the area of the circle inscribed in the star is b a − 3 π for integers a and b , find a b .
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
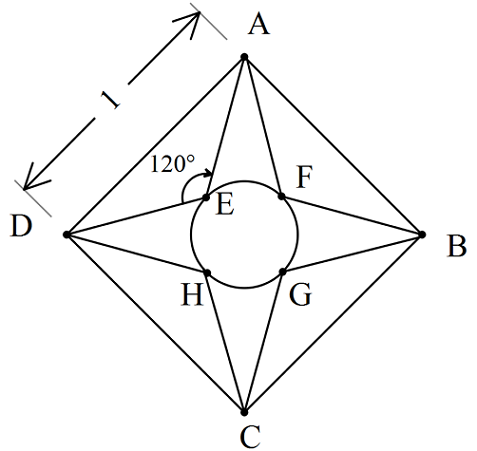
Let us first label the points A to G as shown above.
We want to find the area of the circle that passes through the points E , F , G and H .
Since the figure is symmetric about the lines A C and D B , then A D = A E = A F = F B = D H = H C = C G = G B . And E F = F G = H G = E H .
For simplicity sake, let t = D E = A E > 0 and u = E F = F G > 0 .
Looking at the triangle A E D , and applying cosine rule gives
( D E ) 2 + ( A E ) 2 − 2 ( D E ) ( A E ) cos ( 1 2 0 ∘ ) = A D 2 ⇒ 2 t 2 ( 1 − cos 1 2 0 ∘ ) = 1 ⇒ t = 3 1 .
Because the triangle A D E is isosceles, then ∠ A D E = ∠ D A E = 2 1 8 0 ∘ − 1 2 0 ∘ = 3 0 ∘ . Similarly, ∠ F A B = 3 0 ∘ , so ∠ E A F = 9 0 ∘ − 3 0 ∘ − 3 0 ∘ = 3 0 ∘ .
Looking at the triangle A E F and applying the cosine rule once more gives
( A E ) 2 + ( A F ) 2 − 2 ( A E ) ( A F ) = ( E F ) 2 ⇒ 2 t 2 ( 1 − cos 3 0 ∘ ) = u 2 ⇒ u 2 = 3 2 − 3 .
Finally, let r and d denote the radius and diamater of the circle in question. The area of the circle is
π r 2 = π ( 2 d ) 2 = 4 π d 2 = 4 π [ ( E F ) 2 + ( F G ) 2 ] = 4 π ( 2 u 2 ) = 2 π ⋅ 3 2 − 3 = 6 2 − 3 π .
The penultimate step follows from Pythagorean theorem . Our answer is 2 × 6 = 1 2 .
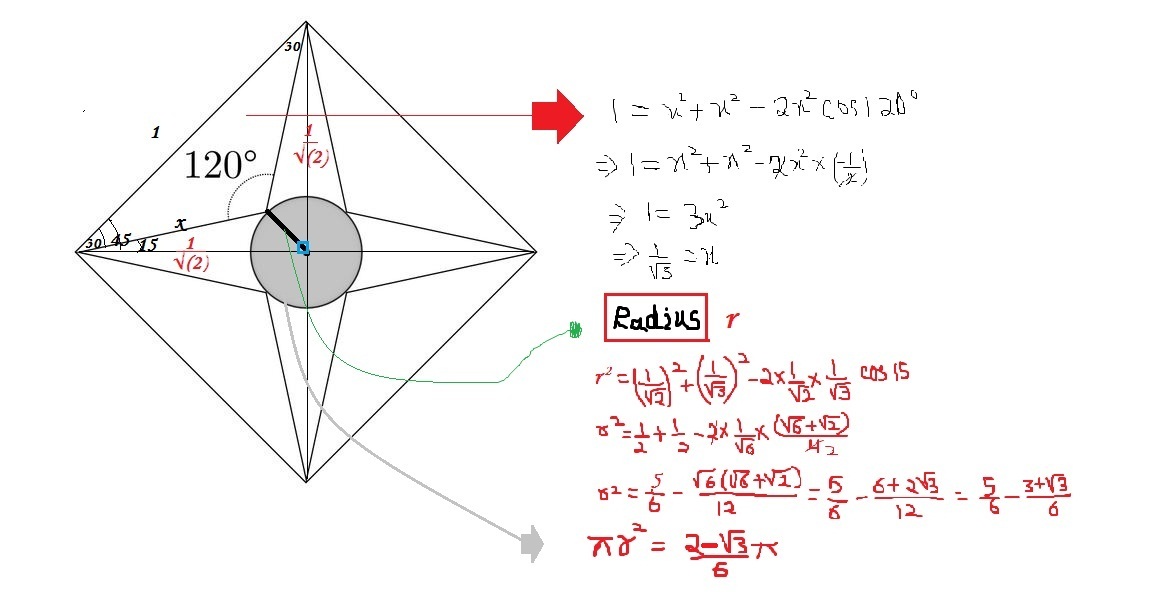
If we draw a line (from side to side in the diamond) through the marked vertex and the opposite point (vertex of the opposite triangle) on the circle, we will find (due to symmetry), that the line is parallel to 2 sides of the rhombus (and therefore, its lenght is 1 (same as the side lenght of the diamond), it goes through the centre of the circle (the part inside the circle is a diameter), and its parts outside the circle form the altitudes of the two isosceles triangles.
These altitudes (h) can be calculated easily (e.g. from the 30-60-90 half triangles):
h = 0 . 5 × t a n 3 0 ° = 6 3
Radius of the circle (r):
2h + 2r =1
r = 0.5 - h
r = 6 3 − 3
Area of the circle:
r 2 π = 3 6 1 2 − 6 3 π = 6 2 − 3 π
Hence, a = 2 , b = 6 and our answer should be
a b = 2 × 6 = 1 2
Find the base of the isosceles triangle ( one of the hand of the star) and due to symmetry the quadrilateral inscribed in the circle is a square then find the radius and tpye your answer. Phewwwww.....😢
Can you elaborate on it?
I will post a proper sol. As quick as possible but for now I found the side of the square incribed in the circle using sine rules and then for radius used the formula s=2r sin(π/4). Where r is radius of the circle and s is sq side
And u can easily check that given diamond is s square
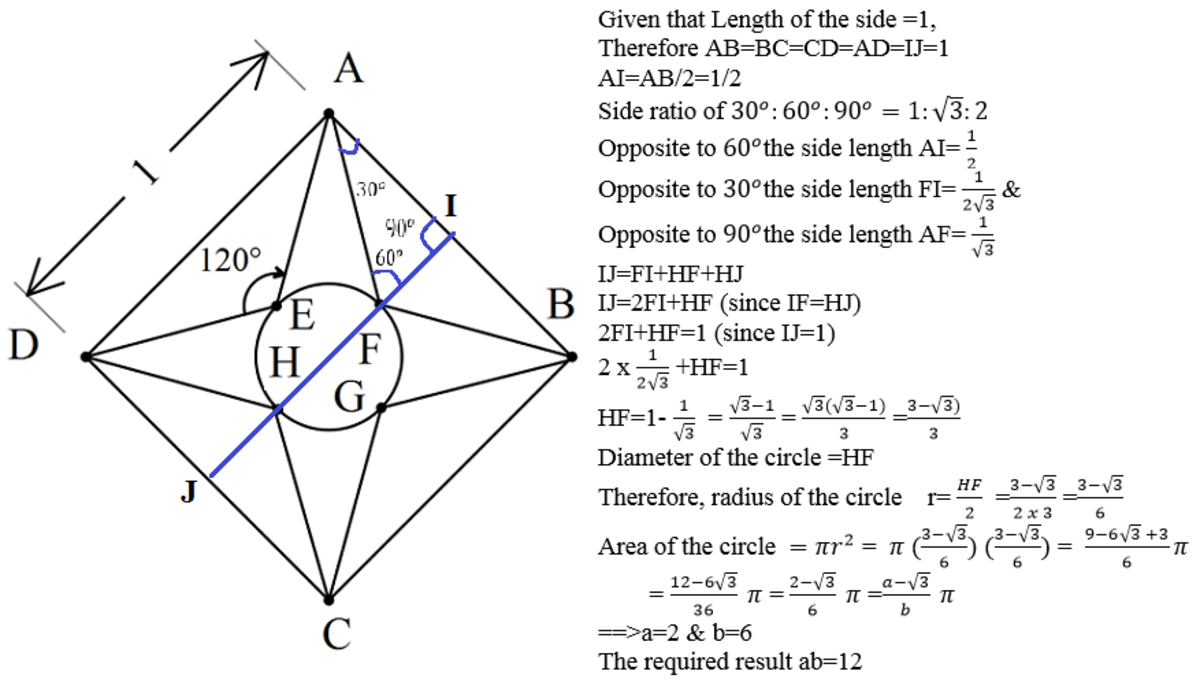
Since the circle is placed right the center of the square and the figure is symmetrical, then the red straight line A D passes through the center of the circle and has a length equal to the side length of the square, A D = 1 .
With A and D passes through the midpoints of the side lengths of the square, then E D = 1 / 2 and ∠ E C D = 2 1 2 0 ∘ = 6 0 ∘ . So tan ( ∠ E C D ) = C D E D ⇒ 3 = C D 1 / 2 ⇒ A B = C D = 2 3 1 .
Thus, the diameter of the circle is d = A D − A B − C D = 1 − 2 ( 2 3 1 ) = 1 − 3 1 .
Hence, the area of the circle is π r 2 = π ( 2 d ) 2 = 4 π ( 1 − 3 1 ) 2 = 6 2 − 3 π .
Our answer is 2 × 6 = 1 2 .