Median of Square's Area
The length ( L ) and width ( W ) of a rectangle are random variables, independently and uniformly distributed on the interval [ 9 , 1 1 ] , and the area ( A ) of the rectangle is also a random variable: L , W ∼ U ( 9 , 1 1 ) ; A = L W . It is not difficult to see that the expected value of the area is E [ A ] = 1 0 0 .
Determine the median of the area.
The answer is 99.6773.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
This is the best and most elegant answer. (I am biased because I did it the same way!)
Same answer!
We will determine the probability function F A ( a ) = P ( A < a ) . The median is then the value m for which F A ( m ) = 0 . 5 .
The distributions for W and L have probability function F W , L ( x ) = ⎩ ⎪ ⎨ ⎪ ⎧ 0 2 1 ( x − 9 ) 1 x < 9 9 ≤ x ≤ 1 1 x > 1 1 f W , L ( x ) = F W , L ′ ( x ) = ⎩ ⎪ ⎨ ⎪ ⎧ 0 2 1 0 x < 9 9 ≤ x ≤ 1 1 x > 1 1 In principle, F A ( a ) = P ( A < a ) = ∬ ℓ w = a f W ( w ) f L ( ℓ ) d w d ℓ = ∫ 9 1 1 2 1 F L ( a / w ) d w . If a < 8 1 , we have a / w < 9 on the entire integration interval, so that F A ( a ) = 0 .
If a > 1 2 1 , we have a / w > 1 1 on the entire integration interval, so that F A ( a ) = ∫ 9 1 1 2 1 ⋅ 1 d w = 1 .
If 8 1 ≤ a ≤ 9 9 , then a / w < 1 1 on the entire integration interval, but a / w < 9 for w > a / 9 . Therefore we have F A ( a ) = ∫ 9 a / 9 4 1 ( w a − 9 ) d w = 4 1 [ a ln w − 9 w ] 9 a / 9 = 4 1 ( a ln a − 2 a ln 9 + 8 1 − a ) .
If 9 9 ≤ a ≤ 1 2 1 , then a / w > 9 on the entire integration interval, but a / w > 1 1 for w < a / 1 1 . Therefore we have F A ( a ) = 1 − ∫ a / 1 1 1 1 4 1 ( 1 1 − w a ) d w = 1 − 4 1 [ 1 1 w − a ln w ] a / 1 1 1 1 = 4 1 ( 2 a ln 1 1 − a ln a + 1 1 7 − a ) .
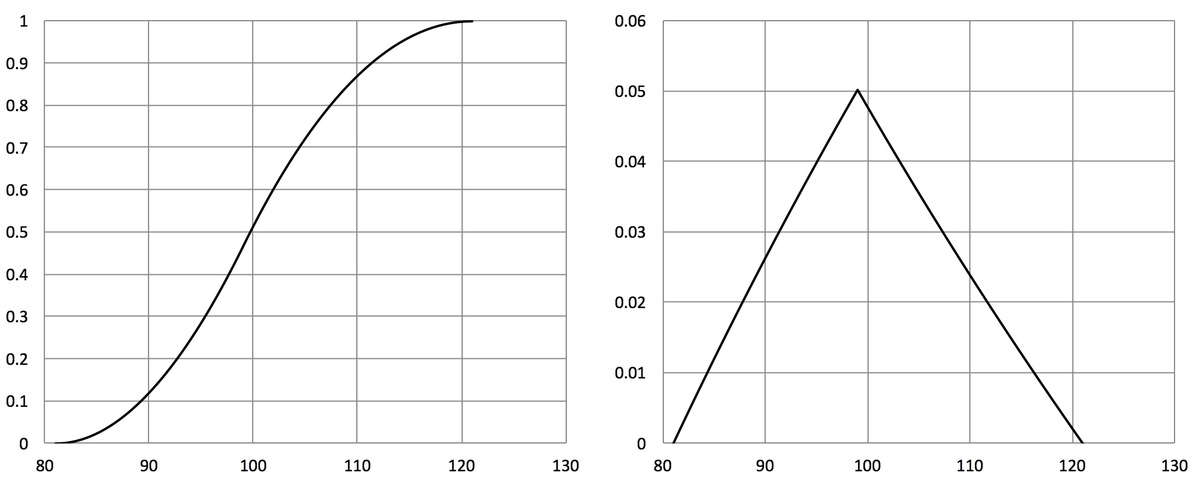
Thus the probability function for the area is F A ( a ) = ⎩ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎧ 0 4 1 ( a ln a − 2 a ln 9 + 8 1 − a ) 4 1 ( 2 a ln 1 1 − a ln a + 1 1 7 − a ) 1 a < 8 1 8 1 ≤ a ≤ 9 9 9 9 ≤ a ≤ 1 2 1 a > 1 2 1 At the transition point F A ( 9 9 ) ≈ 0 . 4 6 6 6 0 0 ; the median is therefore greater than 99, and we solve numerically 4 1 ( 2 a ln 1 1 − a ln a + 1 1 7 − a ) = 0 . 5 2 a ln 1 1 − a ln a + a = 1 1 9 ∴ m = a ≈ 9 9 . 6 7 7 3 .
Graphs of the probability function F A and probability density function f A = F A ′ :
How is the median of a random variable defined?
Log in to reply
Given a random variable X , determine x − and x + such that x − = sup { P ( X ≤ x ) < 2 1 } ; x + = inf { P ( X ≥ x ) < 2 1 } . The median is the mean of these two values, med X = 2 1 ( x − + x + ) .
In many cases, it is simply the unique value x for which P ( X ≤ x ) = 2 1 , i.e. F X ( x ) = 2 1 . The technical details in the definition are necessary if there is no such unique value.
I have a question. Why do you divide by 4 in the integral ∫ 9 9 a 4 1 ( w a − 9 ) d w when the length of the interval is 1 1 − 9 = 2 ?
Log in to reply
The first factor 2 1 comes from the probability function for the length, F ( ℓ ) = 2 1 ( ℓ − 9 ) . The second factor 2 1 comes from the probability density for the width, f ( w ) = 2 1 .
Or, the random variable vector ( L , W ) is uniformly distributed over [ 9 , 1 1 ] × [ 9 , 1 1 ] , a square of area four. In order for the total probability to be one, we need d P ( ℓ , w ) = 4 1 d ℓ d w .
Also, I think you made a little mistake while integrating. For example, the first part of the CDF I think should be 4 1 ( a ln ( a ) − 2 a ln 9 − a + 8 1 )
Mean (81,121) = 101 this is wrong answer .. but the app allows it
You should mention this in the "Reports" section, not the solutions section.
For each value, we have 3 possible values 9, 10 and 11 As such, the possible outcomes for A are 81 90 99 100 110 121. everything but the squares occur 2 times {90, 99, 110} while the squares occur 1 time {81, 100, 121}.
Therefore the complete set looks like this:
{81, 90, 90, 99, 99, 100, 110, 110, 121} which includes
1 2 3 4 5 6 7 8 9
The result should, therefore, be 99. Even if I made a mistake, the only possible answers could ever be 99 or 99,5 as in (99+100)/2. Whatever was calculated was NOT the mean! It probably was the average, but I'm too lazy to check. Just as I am too lazy to format this here, even if it wouldn't be hard in Latex...
I believe this problem includes all the values between 9 and 11 (eg 9.839385 and 10.40872134) so it isn't as simple as that.
Log in to reply
That is correct. There is no reason to assume that the length or width should be an integer.
You approach is in principle correct. However, there are an infinite number of possible values for the area, which makes taking the median a lot harder. My solution basically boils down to find out "how many times" each of the possible values of the area (anything from 81 to 121) occurs, and picking the middle value of this weighted set of values. But because of the infinite number of possibilities, we need the theory of continuous probability distributions and integral calculus.
An intermediate approach would be as follows: in the interval [ 9 , 1 1 ] , pick (say) 20 equidistance points. Calculate the area for each of these cases. Sort them from low to high and choose the mean of the middle elements. Here is a spreadsheet that does the trick:
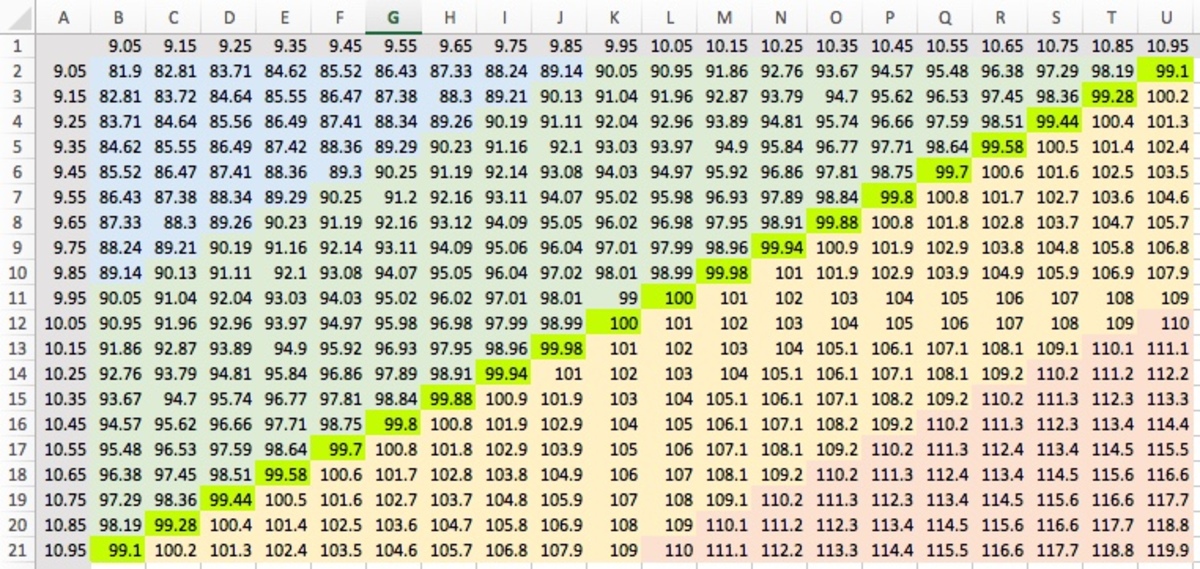
It turns out that the neon green diagonal contains only values in the interval ⟨ 9 9 , 1 0 0 ] ; to the top-left everything is ≤ 9 9 ; to the bottom-right everything is > 1 0 0 . Therefore the median will lie between 99 and 100. Now focus on the values on the diagonal. The run from smallest in the corners to highest in the center. The median of these 20 values (or rather, 10 values, each of which occurs twice!) is the median of the entire table. Thus we take med { 9 9 . 1 , 9 9 . 2 8 , 9 9 . 4 4 , 9 9 . 5 8 , 9 9 . 7 , 9 9 . 8 , 9 9 . 8 8 , 9 9 . 9 4 , 9 9 . 9 8 , 1 0 0 } = 2 9 9 . 7 + 9 9 . 8 = 9 9 . 7 5 . (The values in the spreadsheet are rounded; more accurately, we'd find 9 9 . 7 4 7 5 as the median, which Excel confirms when we type = M E D I A N ( B 2 : U 2 1 ) .)
This is not exact because we picked only 400 possible length/width combinations, while there are infinitely many. Repeating this procedure with 1 0 0 0 0 points, I find the median to be 9 9 . 6 7 9 3 , within 0.01% of the precise value. (Now the values between 99 and 100 no longer lie on a diagonal, but on a slightly curved line; it is part of a hyperbola.)
The solution given above applies Calculus techniques to figure out what happens if we let the number of values in the median calculation approach infinity.
Log in to reply
Thanks for your nice graphical repesentation. :)
In a spreadsheet, 21 rows labeled 9.025 to 10.975 in .05 steps. Same labels for 21 columns. In the grid between them, value equals row label times column label. In a separate cell, put the median function over then entire grid. Answer is 99.68, within the acceptable accuracy of the answer. (If more accuracy is needed, use more steps.)
You may have noticed, my answers tend to be more practical than theoretical.
Shaded areas represent possible values for (L, W). If you can find a curve LW = A bisects the area of this square, then A is the required median.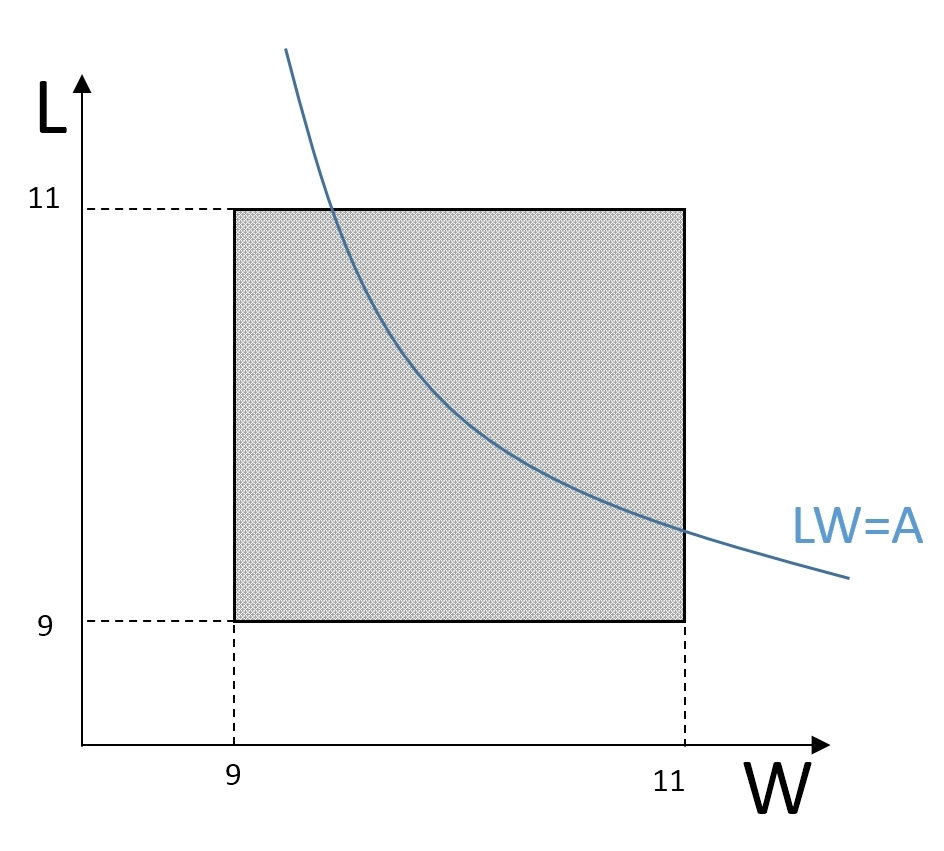 Calculate the shadow area of the upper half, we come to this formula.
Calculate the shadow area of the upper half, we come to this formula.
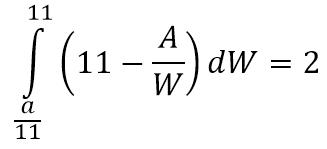 The final solution A = 99.6773
The final solution A = 99.6773