Medians and Sides changed their roles

Geometry Level 5

Let $T_1$ be a scalene triangle whose area is $23$ .
Let $T_2$ be another triangle whose side lengths are equal to the medians of triangle $T_1$ .
Similarly, let $T_3$ be yet another triangle with side lengths equal to the medians of triangle $T_2$ .

Find the area of triangle $T_3$ .

Give your answer to 3 decimal places.

The answer is 12.9375.

4 solutions

Calvin Lin Staff
Jan 4, 2017

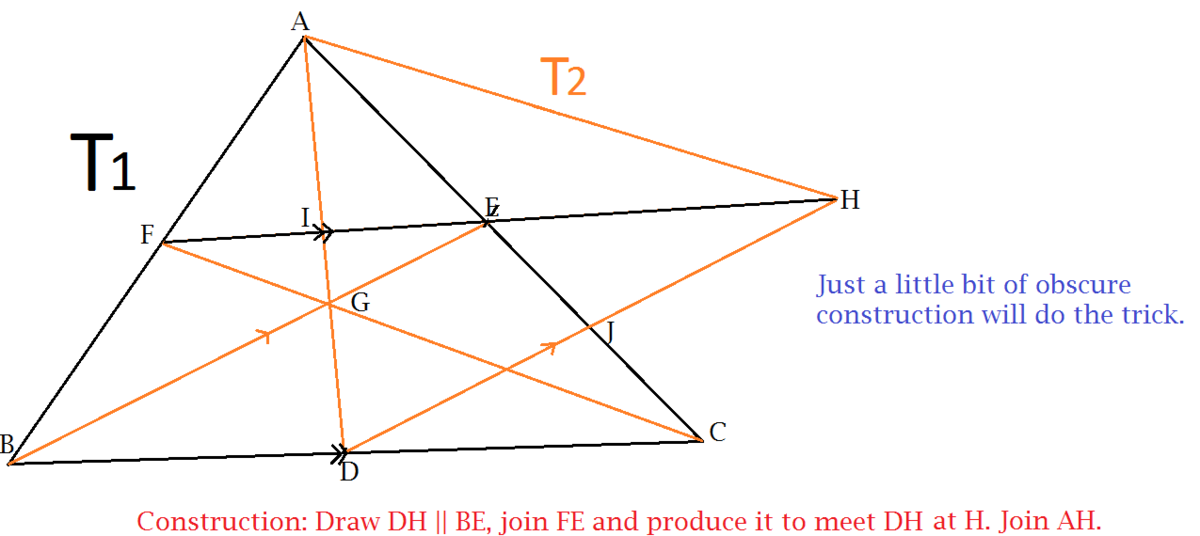
Claim: The triangle T constructed from medians has 3/4 the area of the original triangle S.

Proof using vectors. Let the original triangle S have vertices represented by the vectors $\vec{a}, \vec{b}, \vec{c}$ . The medians are of the form $\vec {a} - \frac{ \vec {b} + \vec {c} } { 2 }$ .
Consider a new triangle whose vertices are represented by $\frac{ \vec{a} - \vec{b} } { 2 } , \frac{ \vec{b} - \vec{c} } { 2 } , \frac{ \vec{c} - \vec{a} } { 2 }$ . We see that the sides are vectorially equal to the median, since $\frac{ \vec{a} - \vec{b} } { 2 } - \frac{ \vec{c} - \vec{a} } { 2 } = \vec {a} - \frac{ \vec {b} + \vec {c} } { 2 }$ , which implies that they have the same length. Hence, this is indeed the triangle T constructed from medians.

Recall that the area of a triangle is given by $\frac{1}{2} \times ( \vec {a} - \vec{b} ) \times ( \vec{b} - \vec{c} ) = \frac{1}{2} ( \vec{a} \times \vec{b} + \vec{b} \times \vec{c} + \vec{c} \times \vec{a} )$ , which is also equal to $\frac{1}{2} \times ( \vec {b} - \vec{c} ) \times ( \vec{c} - \vec{a} )$ and $\frac{1}{2} \times ( \vec {c} - \vec{a} ) \times ( \vec{a} - \vec{b} )$ , Hence, the area of the triangle T is given by $\frac{ 1}{2} \times ( \frac{ \vec{a} - \vec{b} } { 2 } \times \frac{ \vec{b} - \vec{c} } { 2 } + \frac{ \vec{b} - \vec{c} } { 2 } \times \frac{ \vec{c} - \vec{a} } { 2 } + \frac{ \vec{c} - \vec{a} } { 2 } \times \frac{ \vec{a} - \vec{b} } { 2 })$ , which is 3/4 the area of the original triangle.

Vishwash Kumar Γξω
Jan 4, 2017

Relevant wiki: Median

                                                                                                                                                                                              K.I.P.K.I.G

Good ideas! The 2 main steps that we want are:

Show that triangle ADH is the triangle of medians.
Show that area ADH / area ABC = 3/4.

There is a much faster way to arrive at these conclusions. After finding a way to solve the problem, spend some time to figure out the crux and the best way to present the approach. You might be surprised at how much else you can learn from it!

Calvin Lin Staff - 4 years, 5 months ago

I think the core of the question is that construction. We just had to find out those. I see your solution, usins vectors (Nice). I don't really understand Vector but I see that you have written that the sides contructed are "vectorially equal to the medians" which is easy to understand. I have described the similar step which is via geom to help the reader. I think I should remove them in order to make it shorter and easier for the reader to understand. Yep it is a very interesting problem, and makes you relate those things which at random seems to have no relations but it tells us the wideness of mathematics. thanks for your nice suggestions:))))!!!!!!!!!!!!!!!!!!!!!!

Vishwash Kumar ΓΞΩ - 4 years, 5 months ago

Jitarani Nayak
Jan 19, 2018

Projective geometry .
Lemma 1 : A parallel projection preserves the ratio of lengths of two collinear segments.
Lemma 2 : A parallel projection preserve the ratio of the areas of two figures in the plane.

Using this two lemmas we can consider to solve the problem in a parallel projectivity, after the scalene Triangle is projected to an equilateral triangle and still the medians and the ratio of areas are preserved.

It is quite easy to show in equilateral triangle that the ratio of areas scale by a factor of 3/4 each time and finally we get the answer as 12.9375.

Aniruddha Bagchi
Jan 2, 2017

Area of triangle T3 = (3/4)×(3/4)×23 cm2 = 12.93 cm2

Without a legit proof, to me, it just seems to be an educational guess. I would try to add my solution as soon as I get free.

Vishwash Kumar ΓΞΩ - 4 years, 5 months ago

Can you explain why?

Calvin Lin Staff - 4 years, 5 months ago

Medians and Sides changed their roles

The answer is 12.9375.

4 solutions

0 pending reports