Medians to Area of Square
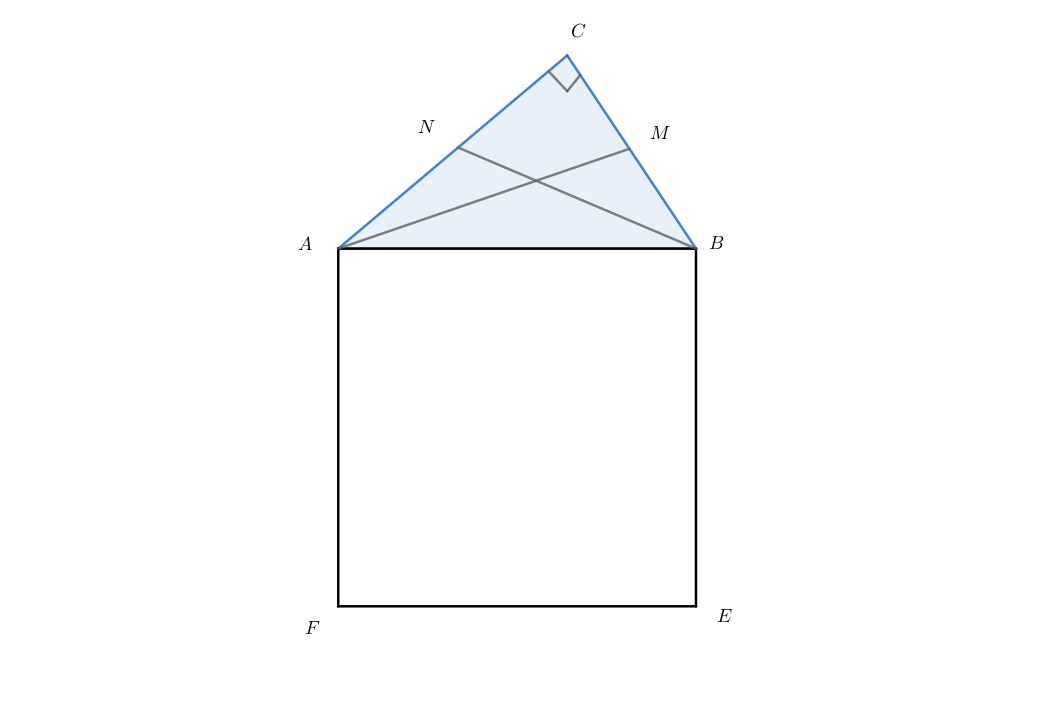
is a right triangle with
and are two medians of .
Find the area of the square .
The answer is 820.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Median divides side into 2 equal halves. Let B C = x and A C = y .
Then,from question, x 2 + ( 2 y ) 2 = 2 5 2 y 2 + ( 2 x ) 2 = 2 0 2 Adding the two equations gives: 4 5 x 2 + 4 5 y 2 = 1 0 2 5 ⇒ 4 5 ( x 2 + y 2 ) = 1 0 2 5 ∴ Area of square ABEF = ( x 2 + y 2 ) 2 = x 2 + y 2 = 1 0 2 5 × 5 4 = 8 2 0