Medium Portion
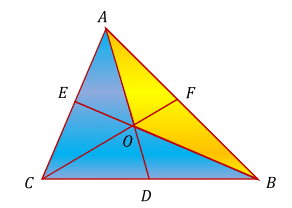 Lines
A
D
,
B
E
,
and
C
F
are medians of triangle
A
B
C
, and the yellow area is
4
7
, how much is the blue area?
Lines
A
D
,
B
E
,
and
C
F
are medians of triangle
A
B
C
, and the yellow area is
4
7
, how much is the blue area?
The answer is 94.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Medians divide the triangle in six triangles of the same area. The yellow area covers two of the six triangles of the same area ∴ the blue area is twice than yellow area ⇒ the blue area is 4 7 × 2 = 9 4
△ A O B and △ A C B have the same base, A B , and their heights are in proportion 3 : 1 since C F = 3 × O F .
Area [ A B C ] = 3 × [ A O B ]
[ b l u e ] = [ A B C ] − [ A O B ] = 2 × [ A O B ] = 2 × 4 7 = 9 4
Actually medians divide △ A B C into six triangles of equal area, in this case four of them are blue and two yellow.
The three medians divide the triangle into six smaller triangles of equal area. Since the yellow area has 2 triangles, the area of one triangle is 2 4 7 = 2 3 . 5 . The blue area has 4 triangles, so the area of the blue area is 4 ( 2 3 . 5 ) = 9 4