Spiraling Down
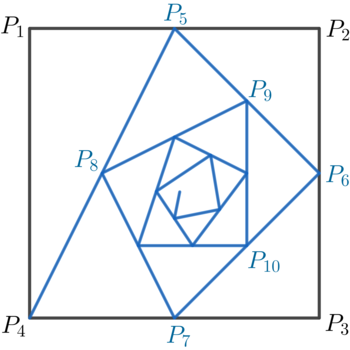
Starting with the vertices P 1 = ( 0 , 1 ) , P 2 = ( 1 , 1 ) , P 3 = ( 1 , 0 ) , P 4 = ( 0 , 0 ) of a square, we construct further points as follows:
- P 5 is the midpoint of P 1 P 2 .
- P 6 is the midpoint of P 2 P 3 .
- P 7 is the midpoint of P 3 P 4 , and so on.
The spiral path approaches a point P ∞ = ( C A , C B ) inside the square, where A , B , C are coprime positive integers.
Find A + B + C .
The answer is 14.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Very nice !
Cool! but shouldn't be, n --> ∞ rather than x --> ∞.
I "solved" this problem numerically, and I'm missing the tools for an exact solution. I figured that
⎣ ⎢ ⎢ ⎡ x 4 i + 1 x 4 i + 2 x 4 i + 3 x 4 i + 4 ⎦ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎡ 0 . 5 0 0 0 . 2 5 0 . 5 0 . 5 0 0 . 2 5 0 0 . 5 0 . 5 0 0 0 0 . 5 0 . 5 ⎦ ⎥ ⎥ ⎤ i ⎣ ⎢ ⎢ ⎡ 0 1 1 0 ⎦ ⎥ ⎥ ⎤
and
⎣ ⎢ ⎢ ⎡ y 4 i + 1 y 4 i + 2 y 4 i + 3 y 4 i + 4 ⎦ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎡ 0 . 5 0 0 0 . 2 5 0 . 5 0 . 5 0 0 . 2 5 0 0 . 5 0 . 5 0 0 0 0 . 5 0 . 5 ⎦ ⎥ ⎥ ⎤ i ⎣ ⎢ ⎢ ⎡ 1 1 0 0 ⎦ ⎥ ⎥ ⎤ .
Now it remaines to calculate n → ∞ lim ⎣ ⎢ ⎢ ⎡ 0 . 5 0 0 0 . 2 5 0 . 5 0 . 5 0 0 . 2 5 0 0 . 5 0 . 5 0 0 0 0 . 5 0 . 5 ⎦ ⎥ ⎥ ⎤ n .
I raised it to high powers with a computer and obtained something which looked a lot like
⎣ ⎢ ⎢ ⎡ 7 1 7 1 7 1 7 1 7 2 7 2 7 2 7 2 7 2 7 2 7 2 7 2 7 2 7 2 7 2 7 2 ⎦ ⎥ ⎥ ⎤ .
Whence ⎣ ⎢ ⎢ ⎡ x ∞ x ∞ x ∞ x ∞ y ∞ y ∞ y ∞ y ∞ ⎦ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎡ 7 1 7 1 7 1 7 1 7 2 7 2 7 2 7 2 7 2 7 2 7 2 7 2 7 2 7 2 7 2 7 2 ⎦ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎡ 0 1 1 0 1 1 0 0 ⎦ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎡ 7 4 7 4 7 4 7 4 7 3 7 3 7 3 7 3 ⎦ ⎥ ⎥ ⎤
Could this have been done rigourously w/o a computer? The Matrix' eigenvalues are far from nice so diagonalization is out of the question.
Anyhow, a very nice problem indeed, thank you!
The eigenvalues aren't nice, but I expressed them in terms of some defined constants so things wouldn't get too hairy. I've just posted a solution using just that method, however, I think Digvijay's method is still the most elegant.
I used a very tedious recurrence method to solve this. Given that P n is the midpoint of P n − 3 and P n − 4 , we have P n = 2 1 ( P n − 3 + P n − 4 ) . Expressing as a matrix, we get
⎝ ⎜ ⎜ ⎛ P n P n − 1 P n − 2 P n − 3 ⎠ ⎟ ⎟ ⎞ = ⎝ ⎜ ⎜ ⎛ 0 1 0 0 0 0 1 0 0 . 5 0 0 1 0 . 5 0 0 0 ⎠ ⎟ ⎟ ⎞ ⎝ ⎜ ⎜ ⎛ P n − 1 P n − 2 P n − 3 P n − 4 ⎠ ⎟ ⎟ ⎞
The transformation matrix has the characteristic polynomial 2 λ 4 − λ − 1 = 0 ,where λ are the eigenvalues. The eigenvalue 1 can be easily factored out, leaving 2 λ 3 + 2 λ 2 + 2 λ + 1 = 0 . Making the substitution λ = t − 3 1 , it can be simplified further to t 3 + 3 2 t + 5 4 1 3 = 0 . From here applying Cardano's formula gives the solutions t = u + v and t = 2 − 1 ( u + v ) ± 2 3 ( u − v ) i , where u = 3 1 0 8 − 1 3 + 1 2 1 3 1 1 , v = 3 1 0 8 − 1 3 − 1 2 1 3 1 1 . Converting back to λ gives us the eigenvalues λ = 1 , λ = u + v − 3 1 and λ = α ± β i where α = 2 − 1 ( u + v ) − 3 1 and β = 2 3 ( u − v ) .
After finding the corresponding eigenvectors for each eigenvalue, the transformation matrix can be expressed as
⎝ ⎜ ⎜ ⎛ 0 1 0 0 0 0 1 0 0 . 5 0 0 1 0 . 5 0 0 0 ⎠ ⎟ ⎟ ⎞ = ⎝ ⎜ ⎜ ⎛ 1 1 1 1 ( u + v − 3 1 ) 3 ( u + v − 3 1 ) 2 ( u + v − 3 1 ) 1 ( α + β i ) 3 ( α + β i ) 2 ( α + β i ) 1 ( α − β i ) 3 ( α − β i ) 2 ( α − β i ) 1 ⎠ ⎟ ⎟ ⎞ ⎝ ⎜ ⎜ ⎛ 1 0 0 0 0 ( u + v − 3 1 ) 0 0 0 0 ( α + β i ) 0 0 0 0 ( α − β i ) ⎠ ⎟ ⎟ ⎞ ⎝ ⎜ ⎜ ⎛ 1 1 1 1 ( u + v − 3 1 ) 3 ( u + v − 3 1 ) 2 ( u + v − 3 1 ) 1 ( α + β i ) 3 ( α + β i ) 2 ( α + β i ) 1 ( α − β i ) 3 ( α − β i ) 2 ( α − β i ) 1 ⎠ ⎟ ⎟ ⎞ − 1
Given that for a matrix A = Q D Q − 1 where D is the diagonal matrix of eigenvalues and Q is the matrix of corresponding eigenvectors, A n can be expressed as Q D n Q − 1 , we can thus express P n as such:
⎝ ⎜ ⎜ ⎛ P n P n − 1 P n − 2 P n − 3 ⎠ ⎟ ⎟ ⎞ = ⎝ ⎜ ⎜ ⎛ 1 1 1 1 ( u + v − 3 1 ) 3 ( u + v − 3 1 ) 2 ( u + v − 3 1 ) 1 ( α + β i ) 3 ( α + β i ) 2 ( α + β i ) 1 ( α − β i ) 3 ( α − β i ) 2 ( α − β i ) 1 ⎠ ⎟ ⎟ ⎞ ⎝ ⎜ ⎜ ⎛ 1 n − 7 0 0 0 0 ( u + v − 3 1 ) n − 7 0 0 0 0 ( α + β i ) n − 7 0 0 0 0 ( α − β i ) n − 7 ⎠ ⎟ ⎟ ⎞ ⎝ ⎜ ⎜ ⎛ 1 1 1 1 ( u + v − 3 1 ) 3 ( u + v − 3 1 ) 2 ( u + v − 3 1 ) 1 ( α + β i ) 3 ( α + β i ) 2 ( α + β i ) 1 ( α − β i ) 3 ( α − β i ) 2 ( α − β i ) 1 ⎠ ⎟ ⎟ ⎞ − 1 ⎝ ⎜ ⎜ ⎛ P 7 P 6 P 5 P 4 ⎠ ⎟ ⎟ ⎞
Since ∣ ∣ u + v − 3 1 ∣ ∣ , ∣ α ± β i ∣ < 1 , the limit as n → ∞ gives ⎝ ⎜ ⎜ ⎛ P ∞ P ∞ P ∞ P ∞ ⎠ ⎟ ⎟ ⎞ = ⎝ ⎜ ⎜ ⎛ 1 1 1 1 ( u + v − 3 1 ) 3 ( u + v − 3 1 ) 2 ( u + v − 3 1 ) 1 ( α + β i ) 3 ( α + β i ) 2 ( α + β i ) 1 ( α − β i ) 3 ( α − β i ) 2 ( α − β i ) 1 ⎠ ⎟ ⎟ ⎞ ⎝ ⎜ ⎜ ⎛ 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ⎠ ⎟ ⎟ ⎞ ⎝ ⎜ ⎜ ⎛ 1 1 1 1 ( u + v − 3 1 ) 3 ( u + v − 3 1 ) 2 ( u + v − 3 1 ) 1 ( α + β i ) 3 ( α + β i ) 2 ( α + β i ) 1 ( α − β i ) 3 ( α − β i ) 2 ( α − β i ) 1 ⎠ ⎟ ⎟ ⎞ − 1 ⎝ ⎜ ⎜ ⎛ P 7 P 6 P 5 P 4 ⎠ ⎟ ⎟ ⎞ ⎝ ⎜ ⎜ ⎛ P ∞ P ∞ P ∞ P ∞ ⎠ ⎟ ⎟ ⎞ = 2 7 u 3 + 2 7 v 3 + 1 0 8 u v − 6 4 1 ⎝ ⎜ ⎜ ⎛ − 2 7 − 2 7 − 2 7 − 2 7 − 2 7 − 2 7 − 2 7 − 2 7 8 1 u v − 9 8 1 u v − 9 8 1 u v − 9 8 1 u v − 9 2 7 u 3 + 2 7 v 3 + 2 7 u v − 1 2 7 u 3 + 2 7 v 3 + 2 7 u v − 1 2 7 u 3 + 2 7 v 3 + 2 7 u v − 1 2 7 u 3 + 2 7 v 3 + 2 7 u v − 1 ⎠ ⎟ ⎟ ⎞ ⎝ ⎜ ⎜ ⎛ P 7 P 6 P 5 P 4 ⎠ ⎟ ⎟ ⎞ Now, putting in the values of the coordinates of P 4 to P 7 gives P ∞ = ( 7 4 , 7 3 )
x1,y1=0,1 x2,y2=1,1 x3,y3=1,0 x4,y4=0,0 c=0 while(c<=5000): x1,y1=(x1+x2)/2,(y1+y2)/2 x2,y2=(x2+x3)/2,(y2+y3)/2 x3,y3=(x3+x4)/2,(y3+y4)/2 x4,y4=(x4+x1)/2,(y4+y1)/2 c+=1 print (x1,y1) //Some Python!!!
Since P n is defined as the midpoint of P n − 4 P n − 3 , x n = 2 1 ( x n − 4 + x n − 3 ) for n ≥ 5 .
So we prove by induction that 2 1 x n + x n + 1 + x n + 2 + x n + 3 = 2
The case n = 1 is immediate, since 2 1 ⋅ 0 + 1 + 1 + 0 = 2
Assume that the result holds for n = k − 1 , that is, 2 1 x k − 1 + x k + x k + 1 + x k + 2 = 2 . Then for n = k ,
2 1 x k + x k + 1 + x k + 2 + x k + 3 = 2 1 x k + x k + 1 + x k + 2 + 2 1 ( x k + 3 − 4 + x k + 3 − 3 ) [by above] = 2 1 x k − 1 + x k + x k + 1 + x k + 2 = 2 [by the induction hypothesis]
Similarly for n ≥ 5 , y n = 2 1 ( y n − 4 + y n − 3 ) , so the same argument as above holds for y , with 2 replaced by
2 1 y 1 + y 2 + y 3 + y 4 = 2 1 ⋅ 1 + 1 + 0 + 0 = 2 3 .
So 2 1 y n + y n + 1 + y n + 2 + y n + 3 = 2 3 for all n .
n → ∞ lim ( 2 1 x n + x n + 1 + x n + 2 + x n + 3 ) = 2 1 n → ∞ lim x n + n → ∞ lim x n + 1 + n → ∞ lim x n + 2 + n → ∞ lim x n + 3 = 2
Since all the limits on the left hand side are same, we get 2 7 n → ∞ lim x n = 2 ⟹ n → ∞ lim x n = 7 4
In the same way, 2 7 n → ∞ lim y n = 2 3 ⟹ n → ∞ lim y n = 7 3
So, P ∞ = ( 7 4 , 7 3 ) .