Memories

I'm actually a self - taught person when it comes to math (with a little help of my very latented neighbour).

But, because of that, I sometimes make misconceptions. But is the problem below - the thought I had in my head when I was 10 - one of my misconceptions?

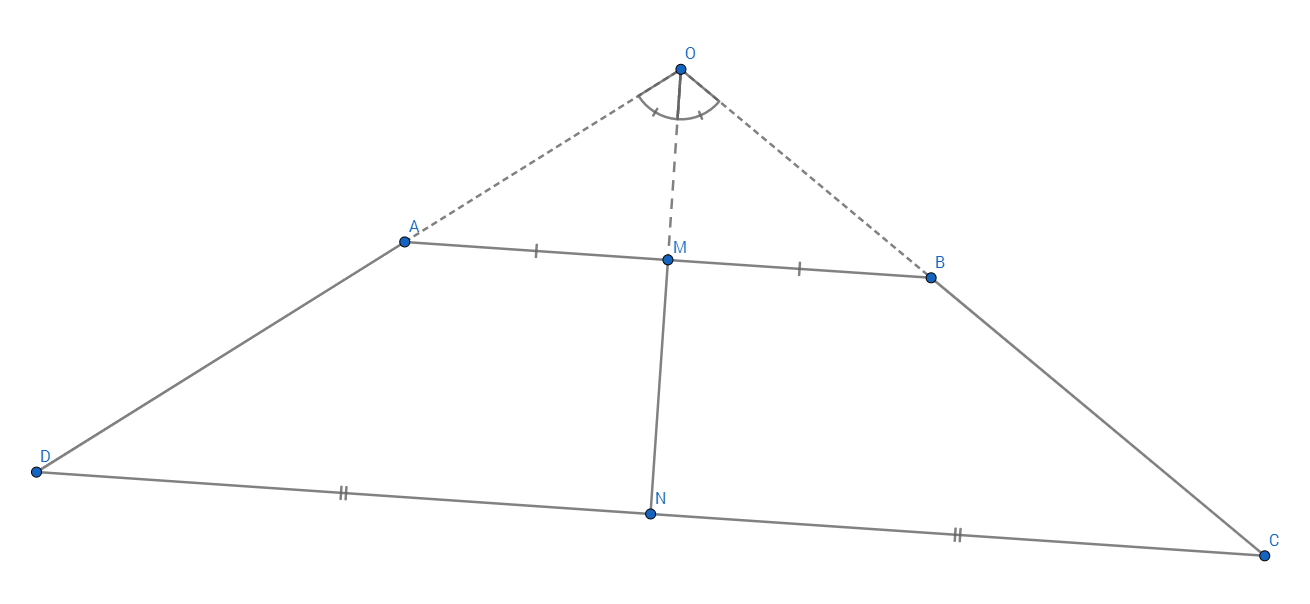
$M$ and $N$ are respectively midpoints of $AB$ and $CD$ - the bases of the trapezoid (or the trapezium) $ABCD$ . Line $BC$ , $DA$ and $MN$ meet at $O$ .

Is it true that line $ON$ is always the bisector of $\widehat{AOB}$ ?

---

This is part of the series: " It's easy, believe me! "