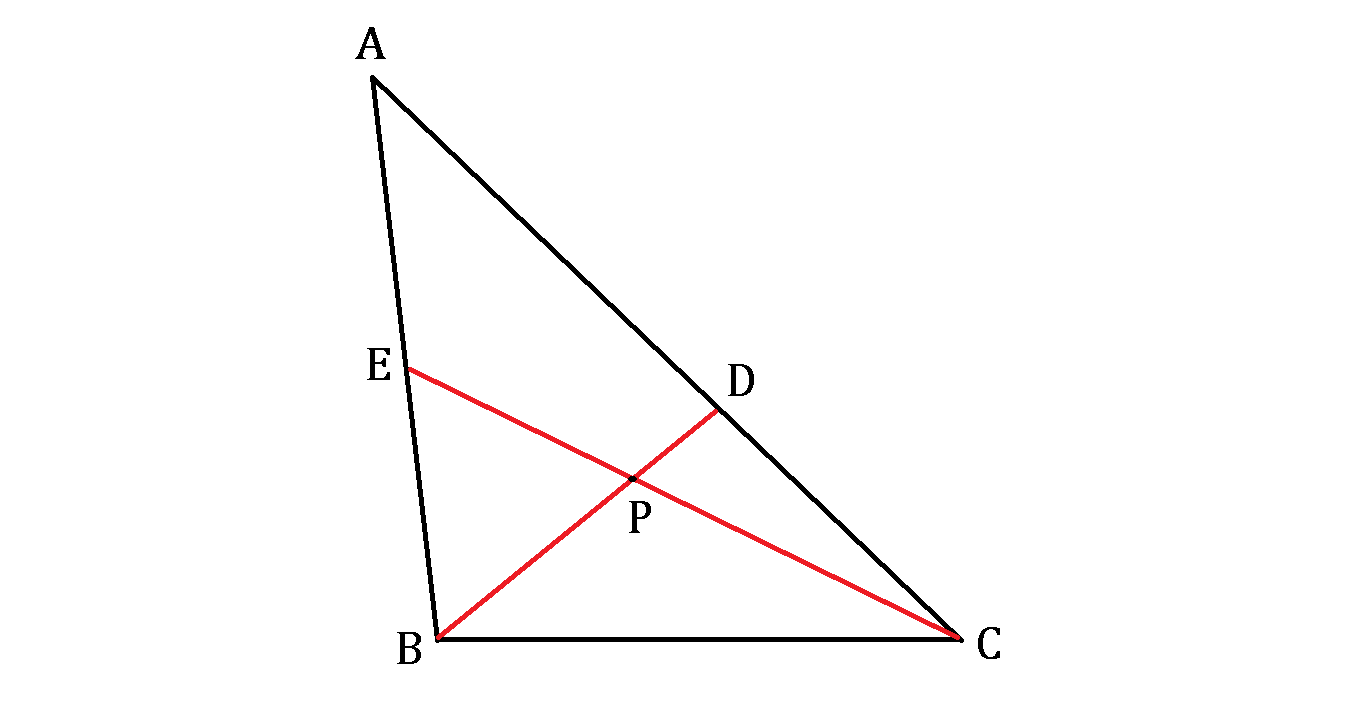
Menelaus' Riddle

Geometry Level 5

Menelaus drew triangle $ABC$ with $BC = 13$ before crossing two red lines $BD = 10$ and $CE = 15,$ both intersecting at point $P$ and reaching the triangle's sides at points $D$ and $E,$ respectively, as shown above.

Menelaus : Mark this, lad. Point $P$ does not only divide all the red segments into integer lengths, but points $D$ and $E$ also divide the triangle's sides into integer lengths.

Pupil : O, so true, master! Any length between any two of those points is always a whole integer!

Menelaus : Then thou shalt tell me. What is the perimeter of triangle $ABC?$

The answer is 50.

1 solution

Niranjan Khanderia
Feb 5, 2017

We use trial and error to find suitable BP and CP, such that DC=(integer) $^2$ and also EB=(integer) $^2$ .
Starting from BP=6, CP=7,8,9. Next BP=7, CP=8 and using Cos Law, as seen in fig 1-2. we get DC=EB=7 an integer.
For these values, as in Fig. 3, AB and AC were also integers, and these values were found.

any one menuluas theorems approach

abhishek alva - 4 years, 3 months ago

Is there any approach without a calculator and tedious calculations.

Bhaskar Pandey - 3 years, 8 months ago

this question is jump ahead any fundamental skills for many newbies .... Olympiad math activated.

Pongkiaet Topar - 3 years, 4 months ago

This theorem is for which class ?

Prateek Sharma - 2 years, 3 months ago

This is for class 9th.

Prateek Sharma - 2 years, 3 months ago

Nice! I used Menelaus' and Stewart's theorem for this problem. Like the solution, I had used to first use trial and error to find the lengths of EP, PC, DP, and PB, and I found the lengths of DC and EB through Stewart's theorem. After this the problem became quite trivial and I just had to find AD and AE using Menelaus' theorem. Really fun problem!

Shubha Gautam - 1 year, 3 months ago

This is damn vague picture

Caishen Stalion - 7 months, 3 weeks ago

Menelaus' Riddle

The answer is 50.

1 solution

0 pending reports