Merrily Swinging Around
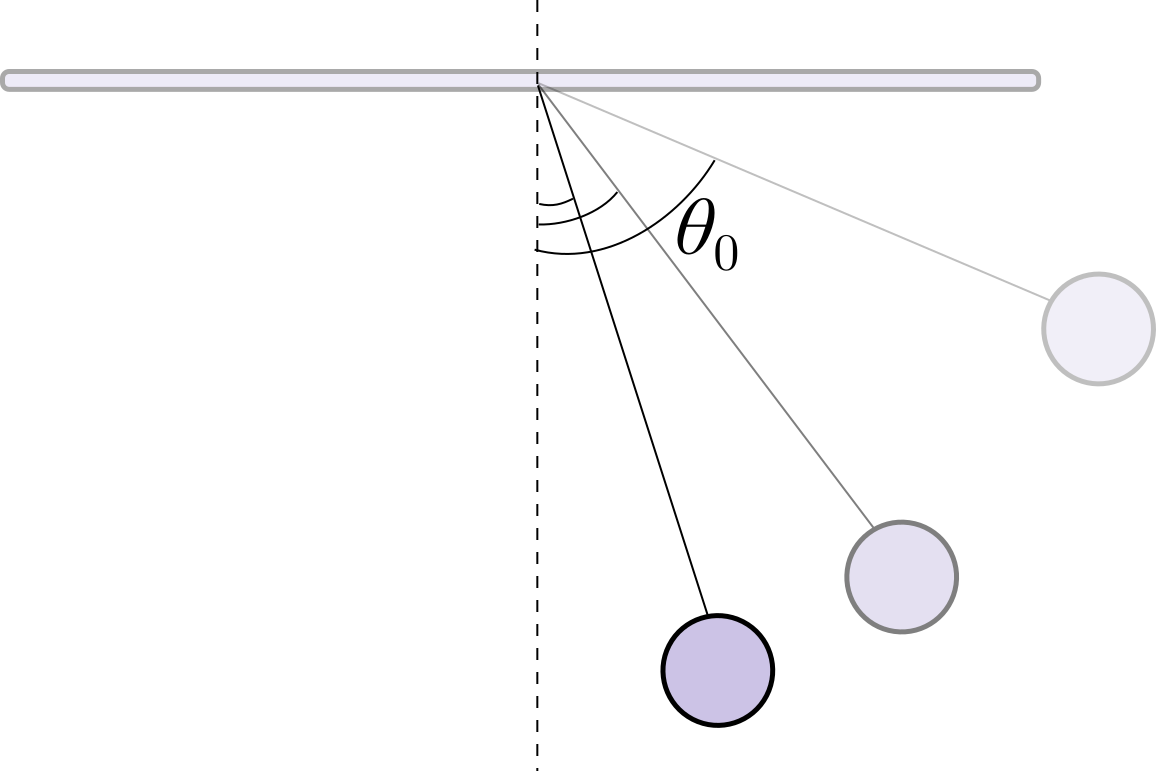
When we swing a pendulum with a small angle, we can approximate its motion to be simple harmonic motion . For a pendulum whose length is , the time period of the pendulum is given by . Note that the time period is independent of the amplitude of oscillation.
Does this result hold true for larger amplitudes as well? How does the time period depend on the amplitude as it goes from to
Note:
Ignore air resistance
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The net torque on the pendulum about the pivot is given by τ = − m g l sin θ . We will use the rotational analogue of Newton's second law motion: net torque ( τ ) is equal to I α .
I α I d t 2 d 2 θ m l 2 d t 2 d 2 θ = − m g l sin θ = − m g l sin θ = − m g l sin θ
We obtain the differential equation
d t 2 d 2 θ = − l g sin θ
We cannot find a closed form solution for this differential equation. However, we can find an infinite series which is sufficient to find the dependence between T and θ .
T = 2 π g l ( 1 + 1 6 1 θ 0 2 + 3 0 7 2 1 1 θ 0 4 + ⋯ )
This is an increasing function since all the coefficients are positive. Thus we see that as θ 0 increases, T also increases, although very slowly.