Messing around with Infinities
Calculus
Level
5
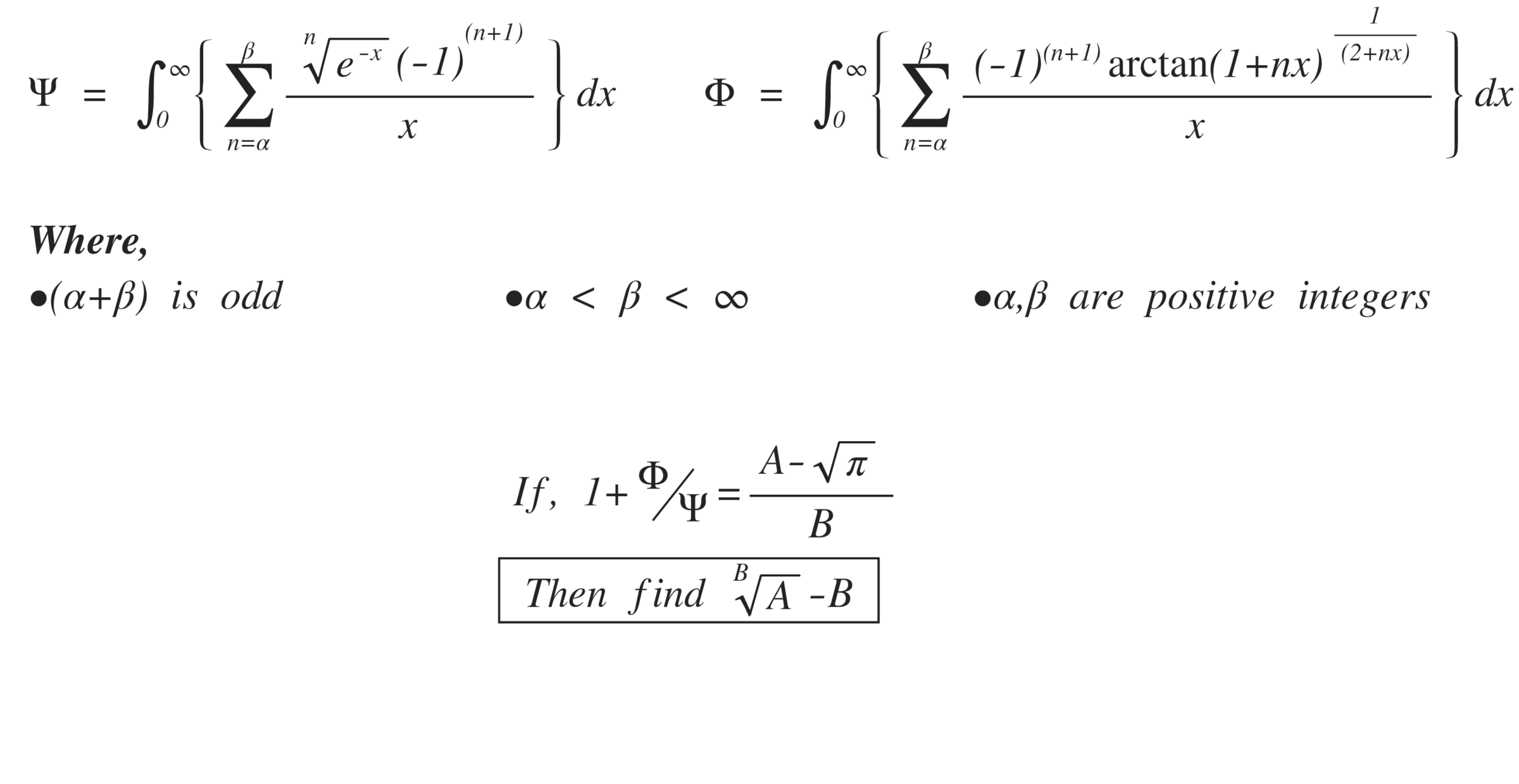
ROUND OFF YOUR ANSWER TO THE NEAREST INTEGER
The answer is 0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Finding Ψ : Let k denote some positive integer. Then ∫ 0 ∞ ( x e − x / ( k + 1 ) − x e − x / k ) d x = ε → 0 + lim ∫ ε ∞ x e − x / ( k + 1 ) d x − ∫ ε ∞ x e − x / k d x = ε → 0 + lim ∫ ε / ( k + 1 ) ∞ u e − u d u − ∫ ε / k ∞ u e − u d u = ε → 0 + lim ∫ ε / ( k + 1 ) ε / k u e − u d u To evaluate this, we note that for any ε > 0 and 0 < u ≤ k ε , we have u e − ε / k ≤ u e − u ≤ u 1 so by integrating, e − ε / k ln ( k k + 1 ) = ∫ ε / ( k + 1 ) ε / k u e − ε / k d u ≤ ∫ ε / ( k + 1 ) ε / k u e − u d u ≤ ∫ ε / ( k + 1 ) ε / k u 1 d u = ln ( k k + 1 ) and taking the limit, ln ( k k + 1 ) = ε → 0 + lim e − ε / k ln ( k k + 1 ) ≤ ε → 0 + lim ∫ ε / ( k + 1 ) ε / k u e − u d u ≤ ε → 0 + lim ln ( k k + 1 ) = ln ( k k + 1 ) . Therefore, we see ∫ 0 ∞ ( x e − x / ( k + 1 ) − x e − x / k ) d x = ε → 0 + lim ∫ ε / ( k + 1 ) ε / k u e − u d u = ln ( k k + 1 ) = ln ( k + 1 ) − ln ( k ) Now note that since α + β is odd, β − α is also odd, so n = α ∑ β x n e − x ( − 1 ) n + 1 = n = 0 ∑ β − α x e − x / ( α + n ) ( − 1 ) α + n + 1 = n = 0 ∑ ( β − α − 1 ) / 2 x e − x / ( α + ( 2 n ) ) ( − 1 ) α + ( 2 n ) + 1 + x e − x / ( α + ( 2 n + 1 ) ) ( − 1 ) α + ( 2 n + 1 ) + 1 = ( − 1 ) α n = 0 ∑ ( β − α − 1 ) / 2 x e − x / ( α + 2 n + 1 ) − x e − x / ( α + 2 n ) From this along with our previous work, we can conclude Ψ = ( − 1 ) α n = 0 ∑ ( β − α − 1 ) / 2 ln ( α + 2 n + 1 ) − ln ( α + 2 n ) = n = α ∑ β ( − 1 ) n + 1 ln ( n )
Finding Φ : Once again, we let k denote some positive integer to write ∫ 0 ∞ ( x ( arctan ( 1 + ( k + 1 ) x ) ) 1 / ( 2 + ( k + 1 ) x ) − x ( arctan ( 1 + k x ) ) 1 / ( 2 + k x ) ) d x = ε → 0 + lim N → ∞ lim ∫ ε N x ( arctan ( 1 + ( k + 1 ) x ) ) 1 / ( 2 + ( k + 1 ) x ) d x − ∫ ε N x ( arctan ( 1 + k x ) ) 1 / ( 2 + k x ) d x = ε → 0 + lim N → ∞ lim ∫ ( k + 1 ) ε ( k + 1 ) N u ( arctan ( 1 + u ) ) 1 / ( 2 + u ) d u − ∫ k ε k N u ( arctan ( 1 + u ) ) 1 / ( 2 + u ) d u = N → ∞ lim ∫ k N ( k + 1 ) N u ( arctan ( 1 + u ) ) 1 / ( 2 + u ) d u − ε → 0 + lim ∫ k ε ( k + 1 ) ε u ( arctan ( 1 + u ) ) 1 / ( 2 + u ) d u Since u → 0 + lim ( arctan ( 1 + u ) ) 1 / ( 2 + u ) = arctan ( 1 ) 1 / 2 = 2 π u → ∞ lim ( arctan ( 1 + u ) ) 1 / ( 2 + u ) = 1 we can once again use the squeeze theorem to show that ε → 0 + lim ∫ k ε ( k + 1 ) ε u ( arctan ( 1 + u ) ) 1 / ( 2 + u ) d u = 2 π ε → 0 + lim ∫ k ε ( k + 1 ) ε u 1 d u = 2 π ln ( k k + 1 ) N → ∞ lim ∫ k N ( k + 1 ) N u ( arctan ( 1 + u ) ) 1 / ( 2 + u ) d u = N → ∞ lim ∫ k N ( k + 1 ) N u 1 d u = ln ( k k + 1 ) and therefore ∫ 0 ∞ ( x ( arctan ( 1 + ( k + 1 ) x ) ) 1 / ( 2 + ( k + 1 ) x ) − x ( arctan ( 1 + k x ) ) 1 / ( 2 + k x ) ) d x = ln ( k k + 1 ) − 2 π ln ( k k + 1 ) = ( 1 − 2 π ) ( ln ( k + 1 ) − ln ( k ) ) Now, using the same method as before, we can conclude Φ = ( 1 − 2 π ) n = α ∑ β ( − 1 ) n + 1 ln ( n )
Finally, we have 1 + Ψ Φ = 1 + n = α ∑ β ( − 1 ) n + 1 ln ( n ) ( 1 − 2 π ) n = α ∑ β ( − 1 ) n + 1 ln ( n ) = 1 + ( 1 − 2 π ) = 2 4 − π so that A = 4 , B = 2 ⟹ B A − B = 4 − 2 = 0