Metallic Spheres
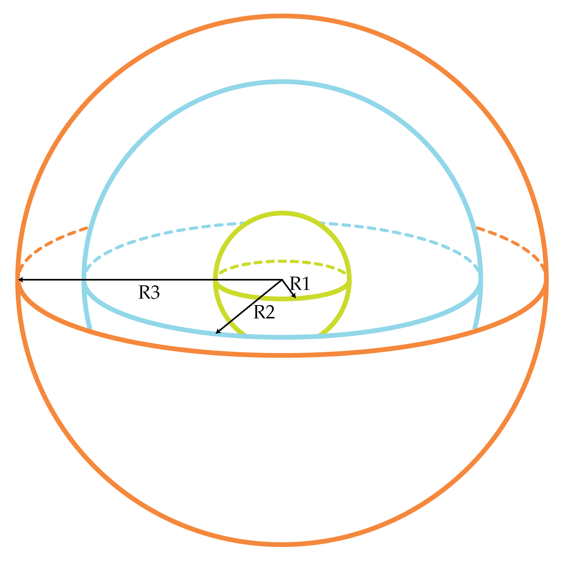
Consider a system of three concentric metallic spheres with radii R 1 = 1 0 c m , R 2 = 3 0 c m and R 3 = 4 0 c m . The inner ( R 1 ) and the outer ( R 3 ) spheres are grounded (they are connected to a large conductor at zero potential ). The relation between the charge Q of the middle sphere and its potential V is linear Q = C s e l f V . The coefficient C s e l f is called self-capacitance. Determine C s e l f in Farads for the middle sphere.
Details and assumptions
k = 4 π ϵ 0 1 = 9 × 1 0 9 m / F
The answer is 1.5E-10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
We start with putting charges on outer and inner surfaces of spheres using the fact that net charge within a conductor is zero. Let outer surface of innermost conductor have charge q . Then using the above fact we find subsequent charges are − q , q ′ , − q ′ , q ′ ′ ( From inside to outside ) . Now applying the fact that inner and outer spheres are grounded ( i.e. their surface potential is zero ) we have the following equations:
1 0 q + 3 0 q ′ − q + 4 0 q ′ ′ − q ′ = 0 − − − ( i )
4 0 q ′ ′ − q ′ + 4 0 q ′ = 0 − − − ( i i )
From ( i i ) we have q " = 0 , which we could also have got from the fact that charge inside a conductor is zero. Plugging this into ( i ) we have q = 8 − q ′ .
Now charge on middle sphere is Q = q ′ − q = 8 9 q ′ and it's potential V = 3 0 × 1 0 − 2 k × q ′ − 4 0 × 1 0 − 2 k × q ′ = 1 2 1 0 × k × q ′ .
So V Q = C s e l f = 1 . 5 × 1 0 − 1 0 .
We can use the fact that this system can be considered to be two spherical capacitors connected in parallel (1,2 and 2,3), since they are at same potential.