Methane in $\mathbb{R}^4$ , Part 2

I will write a solution without using matrices, which will make my work quite a bit longer. I hope the solution will be accessible to those who have not studied Linear Algebra yet.

In what follows, it helps to remember that the angle $\theta$ between two non-zero vectors $v_i$ and $v_j$ in $\mathbb{R}^n$ is defined by $\cos(\theta)=\frac{v_i\cdot v_j}{||v_i||\enspace||v_j||}$ ; in the numerator we take the dot product of $v_i$ and $v_j$ .

Let $v_1,...,v_4$ be four unit vectors in $\mathbb{R}^n$ such that any two of them enclose an angle $\theta$ , meaning that $v_i \cdot v_j=\cos(\theta)$ for $i \neq j$ . Then $(v_1+v_2+v_3+v_4)\cdot (v_1+v_2+v_3+v_4)=4+12\cos(\theta)\geq 0$ , so that $\cos(\theta)\geq -\frac{1}{3}$ .

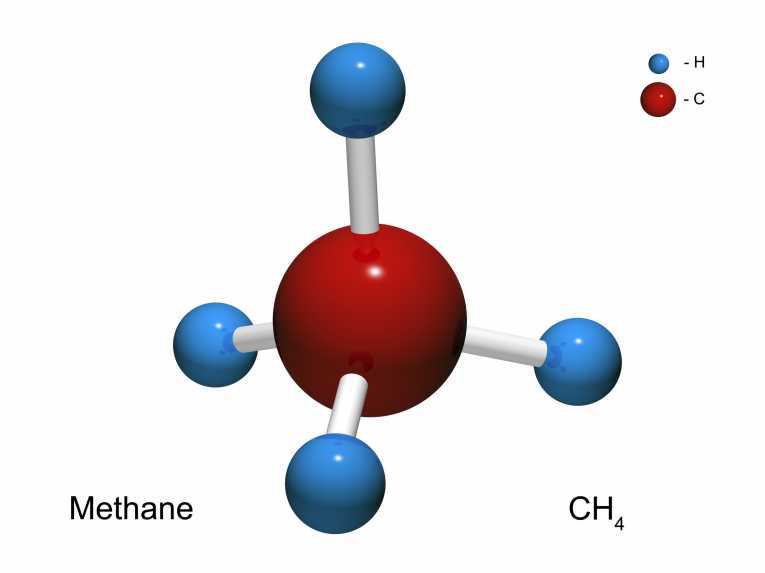
Converely, for every $k$ with $-\frac{1}{3}\leq k \leq 1$ we will show that there exist four nonzero vectors $v_1,..,v_4$ in $\mathbb{R}^4$ such that any two of them enclose an angle $\theta$ with $\cos(\theta)=k$ . Start with four unit vectors $w_1,..,w_4$ in $\mathbb{R}^3$ such that $w_i \cdot w_j=-\frac{1}{3}$ when $i\neq j$ . (You can take the normalized position vectors of the H atoms relative to C in a methane molecule.) Now imbed these vectors into $\mathbb{R}^4$ and choose a vector $w$ orthogonal to the $w_i$ with $||w||^2=a\geq 0$ . Let $v_i=w_i+w$ . If $\theta$ is the angle between $v_i$ and $v_j$ , then $\cos(\theta)=\frac{v_i\cdot v_j}{||v_i||\enspace||v_j||}$ $=\frac{a-\frac{1}{3}}{a+1}$ , which attains all values on the interval $[-\frac{1}{3},1)$ as we let $a$ go from 0 to infinity. If we choose four identical non-zero vectors $v_i$ , then $\cos(\theta)=1$ , of course, showing that the answer is $\boxed{[-\frac{1}{3},1]}$

Bonus: The answer and the solution are the same for $n>4$ : The four vectors we found in $\mathbb{R}^4$ can be imbedded in $\mathbb{R}^n$ for $n>4$ .