Method of image charges (part I)
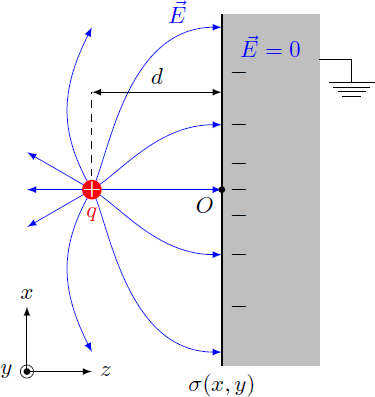
A point charge is located at a distance from a grounded metal plate. Due to electrostatic induction, there is an electric charge density on the metal surface . The surface charges shield the electric field of the point charge, so that within the metal holds.
What is the electric charge density at the origin directly opposite the point charge?
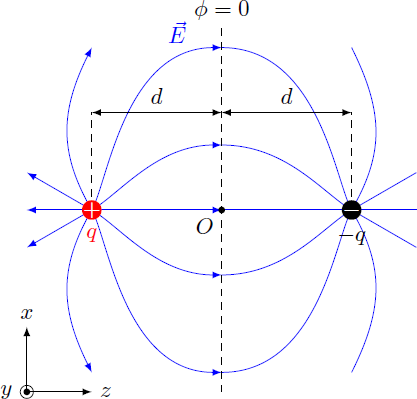
Hint: This problem can be solved with the image charge method. The electric field for our system is the same as for an electric dipole with two point charges (at least for the half space ). In addition to the actual charge at we imagine an image charge at . Use the electric field of this dipole to determine the charge density on the metal surface, that generates the same field.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The electric field of the dipole results E ( x , y , z ) = 4 π ε 0 1 ⎣ ⎡ [ x 2 + y 2 + ( z + d ) 2 ] 3 / 2 q ⎝ ⎛ x y z + d ⎠ ⎞ + [ x 2 + y 2 + ( z − d ) 2 ] 3 / 2 − q ⎝ ⎛ x y z − d ⎠ ⎞ ⎦ ⎤ In the case z = 0 we can simplify the equation to E ( x , y , z = 0 ) = 2 π ε 0 q [ x 2 + y 2 + d 2 ] 3 / 2 d ⎝ ⎛ 0 0 1 ⎠ ⎞ Note that the electric field is perpendicular to the surface z = 0 , so that this is an equipotential surface. Thus, the electric field of the dipole corresponds to the field of the actual charge configuration, since the equipotential surface is the same for both. The only difference is that in the metal E = 0 must apply, so that our solution applies only to the half-space z ≤ 0 .
We can use Gauss's law to calculate the charge density σ ( x , y ) . We integrate the electric field over the surface of a cube d V = d x d y d z centered around the point r = ( x , y , 0 ) . The charge enclosed by the infinitesimal cube is d Q = σ ( x , y ) d x d y .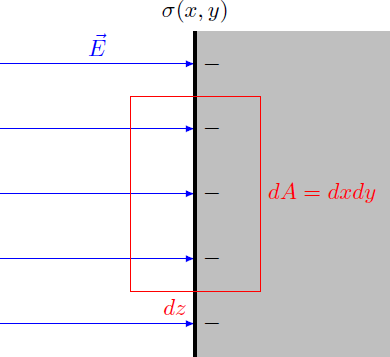 ⇒
⇒
∮
d
V
E
⋅
d
A
−
E
z
(
x
,
y
,
0
)
d
x
d
y
σ
(
x
,
y
)
=
ε
0
d
Q
=
ε
0
σ
(
x
,
y
)
d
x
d
y
=
−
ε
0
E
z
(
x
,
y
,
0
)
=
−
2
π
q
[
x
2
+
y
2
+
d
2
]
3
/
2
d
For
x
=
y
=
0
we get the final result
σ
(
0
,
0
)
=
−
2
π
d
2
q
=
−
2
π
⋅
0
.
2
2
1
0
−
3
m
2
C
≈
−
4
⋅
1
0
−
3
m
2
C
⇒
⇒
∮
d
V
E
⋅
d
A
−
E
z
(
x
,
y
,
0
)
d
x
d
y
σ
(
x
,
y
)
=
ε
0
d
Q
=
ε
0
σ
(
x
,
y
)
d
x
d
y
=
−
ε
0
E
z
(
x
,
y
,
0
)
=
−
2
π
q
[
x
2
+
y
2
+
d
2
]
3
/
2
d
For
x
=
y
=
0
we get the final result
σ
(
0
,
0
)
=
−
2
π
d
2
q
=
−
2
π
⋅
0
.
2
2
1
0
−
3
m
2
C
≈
−
4
⋅
1
0
−
3
m
2
C