Mickey mouse ratios
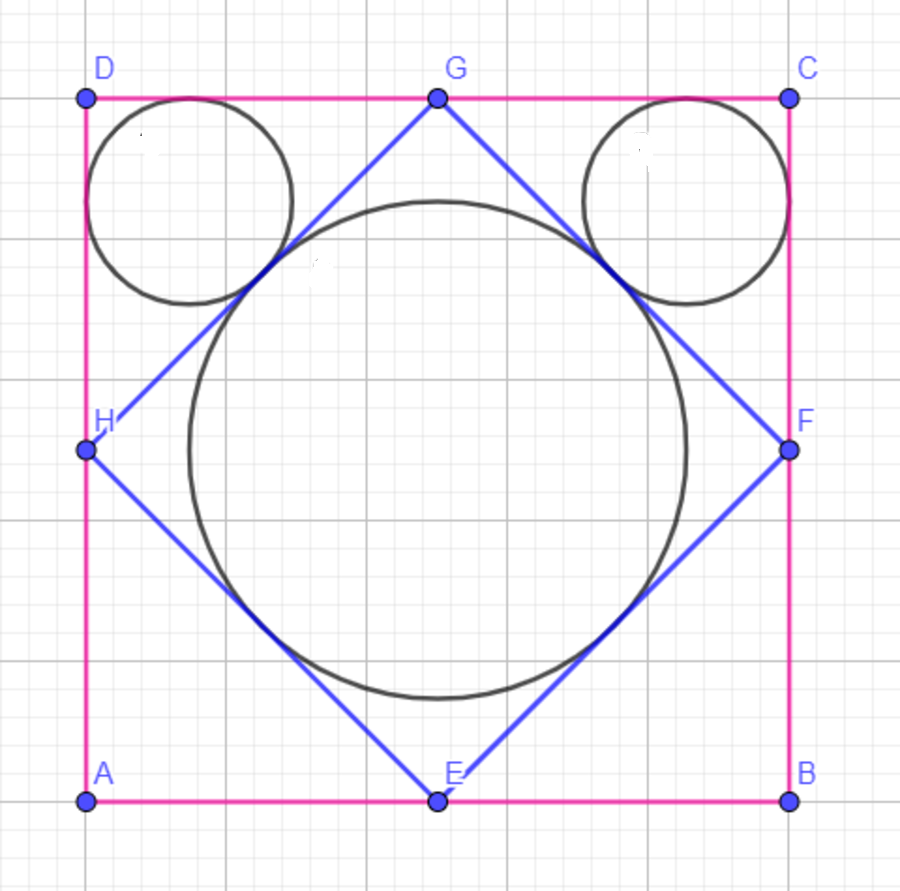
The figure above depicts an outline of Mickey mouse, with the big circle representing his face and the two small circles his ears. Find the ratio of the radius of a small circle to the radius of the big circle, if A B C D is a square, and E , F , G , H are the midpoints of its sides. The answer can be written as a − b . Submit a + b .
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Circle q tangent circle o at I, then
D I 2 r q + r q r o r q = I G = r o = 2 + 1 1 = 2 − 1
Without loss of generality, let the length of the side of the square ABCD be 2. Then, referring to the picture, we see DG = DH = 1 and, by the Pythagorean Theorem, HG = Sqrt(2). If r is the radius of the smaller circle, the formula for the in-radius of a circle shows that:
r = 1 / (2+sqrt(2))
By constructing a line from the center of the big circle to the point of tangency with the little circle, we see that (if R is the radius of the big circle)
R = (1/2)*(HG) = sqrt(2) / 2
Therefore,
r/R = (1/(2+sqrt(2))) / (sqrt(2) / 2) = sqrt(2) - 1.
Hence, a = 2 and b = 1, so that a+b = 3
Note that E F G H is a square. Let the center of square E F G H and the big circle be O , and the side length of square E F G H be 2 , then the radius of the big circle is 1 . Let the center of the top right circle be P and the point it is tangent to the center circle be Q . We note that O , Q , P , and C are colinear. We also note that C Q = O Q = 1 and that C Q = r + 2 r = 1 ⟹ r = 2 + 1 1 = 2 − 1 . Then the ratio of the radius of the small circle to that of the big circle is 1 r = 2 − 1 . Therefore a + b = 2 + 1 = 3 .