Midpoint Approximation
Approximate the area under the curve from 1 to 3 using midpoint rectangles. (MRAM)
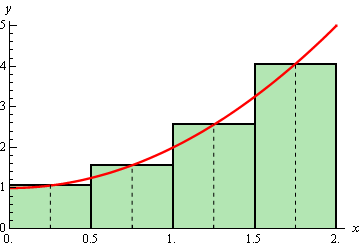
You may use calculator assistance.
The answer is 19.9984.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Derive a summation formula for midpoint approximations.
n ( b − a ) * i = 0 ∑ n − 1 ( f ( a + 2 n ( b − a ) + n ( b − a ) ∗ i ))
Plug in the function x 3 , endpoints a and b , and the number of rectangles n .
5 0 ( 3 − 1 ) * i = 0 ∑ 5 0 − 1 ( ( 1 + 2 ∗ 5 0 ( 3 − 1 ) + 5 0 ( 3 − 1 ) ∗ i ) 3 )
Use a calculator to evaluate this sum which comes out to be 1 9 . 9 9 8 4