Midpoint placement problem

Denote the length of $BD$ by $x$ . Then, $DC=1-x$ . Let $AB=c$ , $AC=b$ , $BC=a=1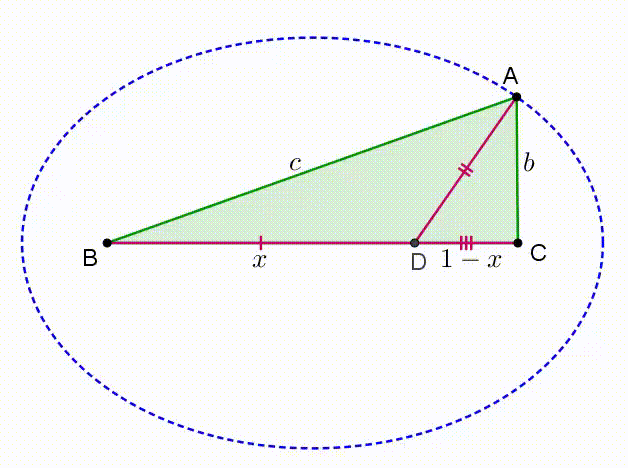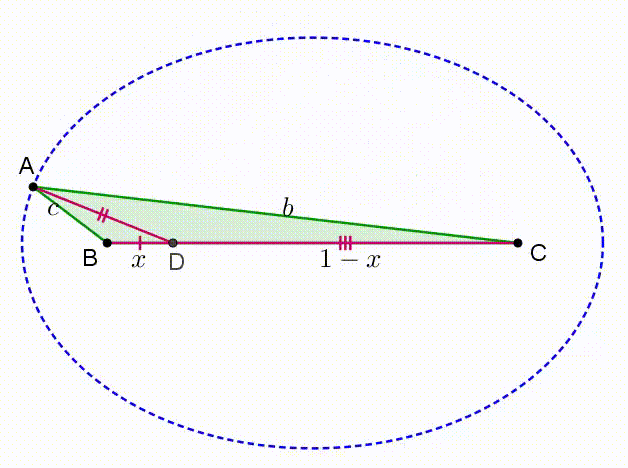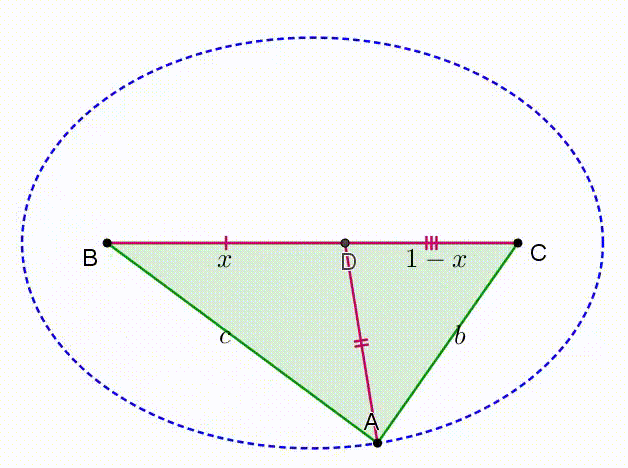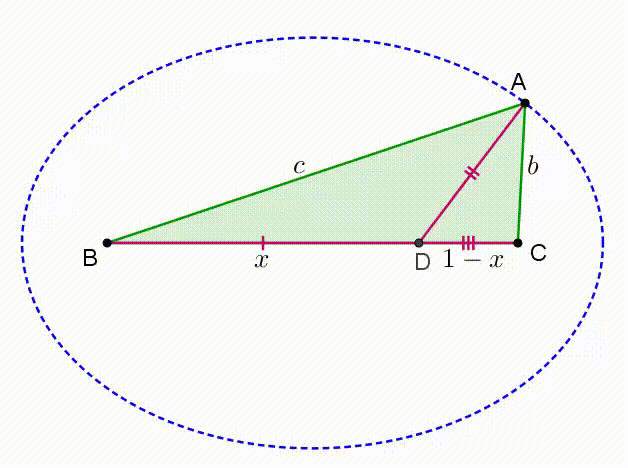$ . It is given that there is a unique value for $x$ , such that $A{{D}^{2}}=BD\cdot DC\Leftrightarrow A{{D}^{2}}=x\left( 1-x \right) \ \ \ \ \ \left(1 \right)$ By Stewart’s theorem ,

$\begin{aligned} & A{{C}^{2}}\cdot BD+A{{B}^{2}}\cdot DC=\left( BD+DC \right)\left( BD\cdot DC+A{{D}^{2}} \right) \\ & \Rightarrow {{b}^{2}}x+{{c}^{2}}\left( 1-x \right)=x\left( 1-x \right)+A{{D}^{2}} \\ & \overset{\left( 1 \right)}{\mathop{\Rightarrow }}\,{{b}^{2}}x+{{c}^{2}}\left( 1-x \right)=x\left( 1-x \right)+{{x}^{2}} \\ & 2{{x}^{2}}+\left( {{b}^{2}}-{{c}^{2}}-2 \right)x+{{c}^{2}}=0 \ \ \ \ \ \left(2 \right)\\ \end{aligned}$ If there were two different values of $x$ satisfying $\left(2 \right)$ , the discriminant of the quadratic equation would be positive. This is not the case, thus,

$\begin{aligned} \Delta =0 & \Leftrightarrow {{\left( {{b}^{2}}-{{c}^{2}}-2 \right)}^{2}}-8{{c}^{2}}=0 \\ & \Leftrightarrow {{\left( {{b}^{2}}-{{c}^{2}}-2 \right)}^{2}}=8{{c}^{2}} \\ & \Leftrightarrow {{b}^{2}}-{{c}^{2}}-2=\pm 2\sqrt{2}c \\ & \Leftrightarrow {{b}^{2}}={{\left( c\pm \sqrt{2} \right)}^{2}} \\ & \Leftrightarrow b=\pm \left( c\pm \sqrt{2} \right) \ \ \ \ \ \left(3 \right)\\ \end{aligned}$ By Triangle Inequality , it holds that $\left| b-c \right|<a\Rightarrow \left| b-c \right|<1$ , hence $\left(3 \right)$ gives only one acceptable relation for positive $b$ and $c$ : $b+c=\sqrt{2}$ This means that there is only one possible perimeter for $\triangle ABC$ : $a+b+c=1+\sqrt{2}\approx \boxed{2.414}$