Midpoint? What About Thirds?
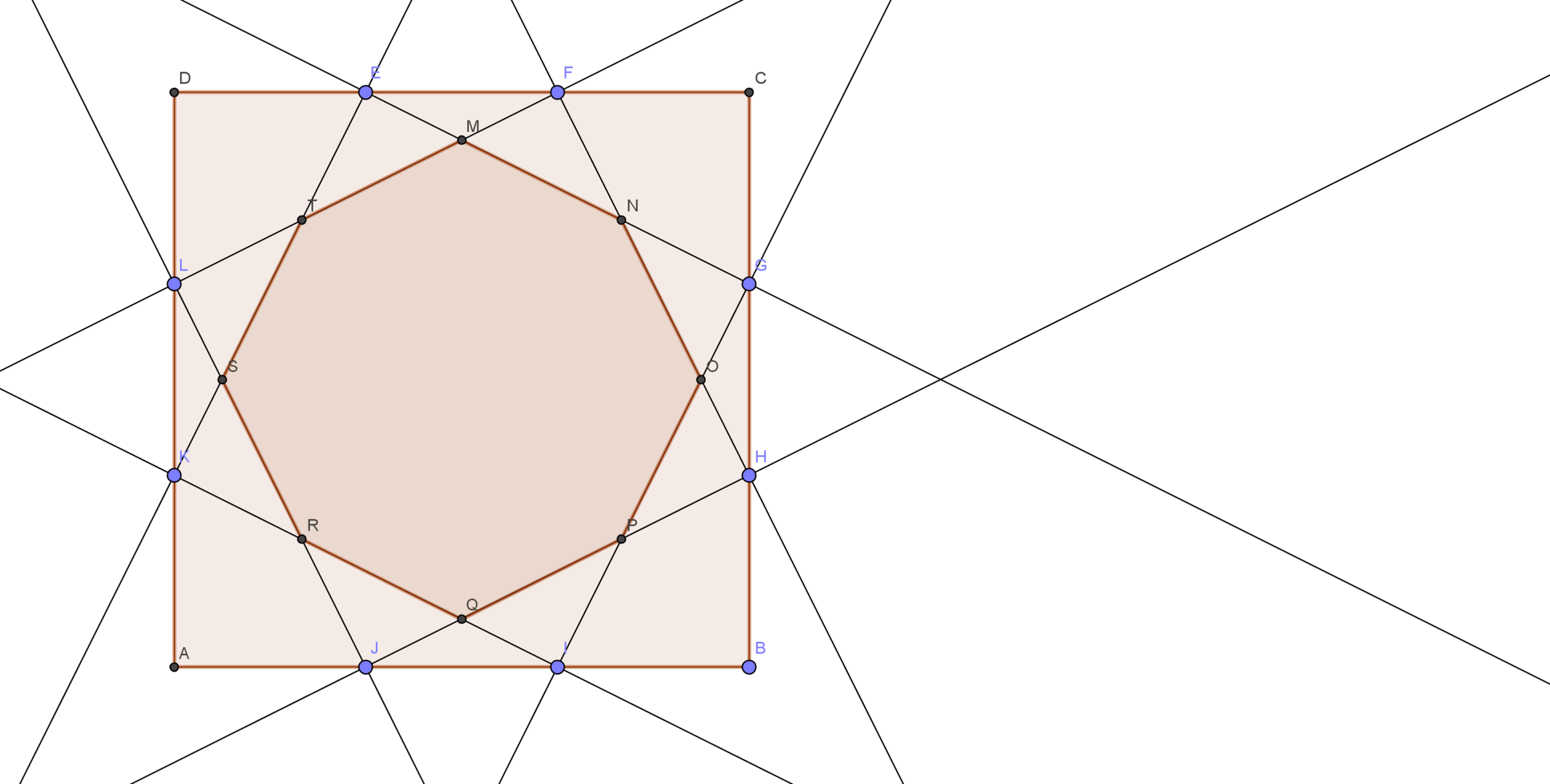 A
B
C
D
is a square with a side length of 18. Divide each side into three equal parts, and mark the points
E
,
F
,
G
,
H
,
I
,
J
,
K
,
L
in a clockwise manner starting from the vertex
D
. Then, connect the points to get a not-necessarily-regular octagon as shown in the figure above. What is the area of the octagon?
A
B
C
D
is a square with a side length of 18. Divide each side into three equal parts, and mark the points
E
,
F
,
G
,
H
,
I
,
J
,
K
,
L
in a clockwise manner starting from the vertex
D
. Then, connect the points to get a not-necessarily-regular octagon as shown in the figure above. What is the area of the octagon?
Bonus : You may notice that the ratio between the segments of all the sides are all 1 : 1 : 1 . Now, generalize this by considering the case of 1 : k : 1 , where k ∈ N .
You may wish to try Part 2 and Part 3 of this trilogy.
The answer is 150.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
I divided the octagon into 4 sub-regions which are symmetrical. And, then I divided one sub-region into two triangles.
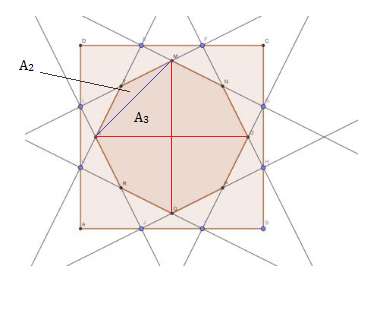 [The picture you provided is somewhat mediocre. Couldn't edit it more.]
[The picture you provided is somewhat mediocre. Couldn't edit it more.]
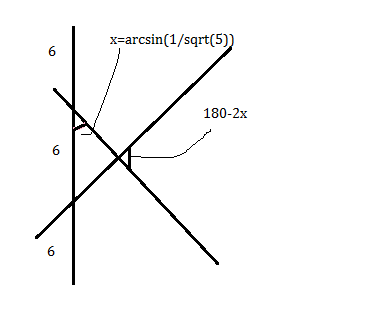
Here, A 3 = 2 1 × ( 2 1 5 ) 2 = 8 2 2 5 And, A 2 = 8 7 5 So, area of one sub-region is 8 3 0 0 Therefore, A t o t = 4 × 8 3 0 0 = 1 5 0
The area of the square (324) can be split into the octagon O, four large right triangles T (w sides 6 & 12), and 4 small right triangles R.
The area of [T] is 36. Now we just need [R].
Let a and b be the legs of R, let x be the smallest angle in T, and let E be the equilateral triangle adjacent to R.
Divide E in half by its altitude, and the resulting triangle is similar to T, with a as it's hypotenuse. By similarity, a=3√5/2.
E has two angles x, so the angle in R next to a is 2x. From T we know tan(x) = 1/2. So tan(2x) = 2tanx/(1-tan²x) = 4/3.
Since b = a tan(2x), this tells us b=4√5/2. So the area [t] = 1/2 ab = 15/2.
Finally, the area [O] = [S] - 4[T] - 4[t] = 324 - 4(36) - 4(15/2) = 150.
————
In general, if each side of the square is (k+2), the same approach yields [S] = (k+2)² 4[T] = 2(k+1) 4[t] = k(1 - k/(k+1)(k+2)) [O] = (k²+k+2) + k²/(k+1)(k+2)
(==> for instance, with the original side length of 18, and a ratio of 1:4:1, [O] would be 202.8)
can anybody use coordinate geometry?, I tried it and got side to be sqrt(109)/2 and area131.57
Log in to reply
I think there should be some calculation mistakes. Coordinate geometry will definately give the correct answer. If I get time I will post a solution based on it.
If possible a diagram would be much helpful. Thank you.
Have a look at Area without Numbers by Victor Paes Plinio
Relevant wiki: Congruent and Similar Triangles
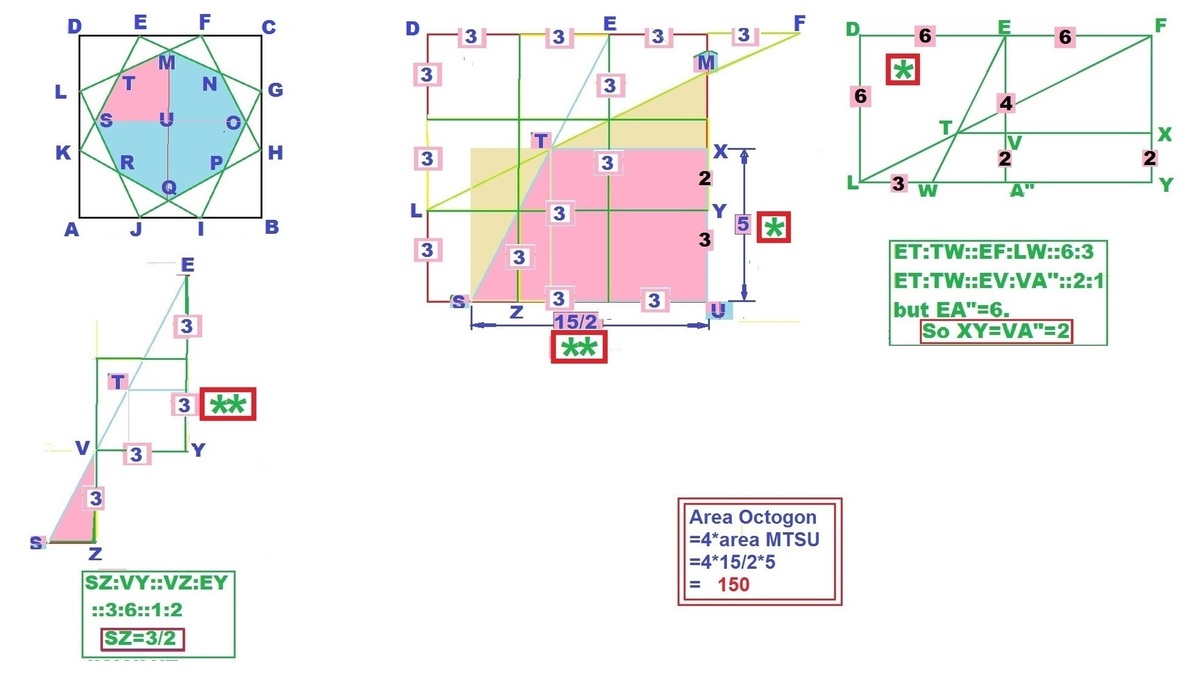
This indeed looks intimidating at the first sight, but instead of finding the darker area, why not we find the lighter area, which is much more easier? First, we see that there are 8 congruent right triangles, namely Δ A K I , Δ H J B , Δ G I B and so on. Since the length of one side is 18, the area covered by the 8 triangles is simply 8 × 2 1 × 1 2 × 6 = 2 8 8 .
But wait! That is not sufficient! There are overlapping areas in between the 8 triangles, and we need to consider that. We now focus on the triangle Q J I , and we can apply the same logic to other congruent triangles, namely Δ M E F , Δ O G H and Δ S L K . Drop a line from Q that is perpendicular to side A B , and we call it Q ′ . Notice that Δ Q Q ′ J is similar to Δ H B J , and in particular, Q ′ is the midpoint of I J , since ∠ Q J I = ∠ Q I J by trigonometry. Since Q ′ J = 2 1 I J = 3 1 Q ′ B = 3 , we conclude that the area of Δ Q J I is just ( 4 1 ) 2 × 7 2 = 4 . 5 . Do this to all other 3 congruent triangles, we get a total area of 1 8 from this case.
There is another intersection in between the right triangles, but this time, it is at the corners of the square, and one of them is P H B I , and we will focus on that. Let P ′ and P ′ ′ be points on A B and B C respectively such that P P ′ and P P ′ ′ are perpendicular to A B and B C respectively. Notice that P P ′ P ′ ′ B is a square due to symmetry, and B P ′ ′ = P P ′ ′ = 2 1 J P ′ due to trigonometry. Solving for P P ′ ′ , we know that P P ′ P ′ ′ B is a square with side length of 4, and I P ′ ′ = H P ′ = 2 . Hence, the area of quadrilateral P H B I is 4 × 4 + 2 × 2 1 × 2 × 4 = 2 4 . Applying the same logic to quadrilaterals D E T L , K R J A and C F N G , and since they are all congruent, we get a total area of 2 4 × 4 = 9 6 in this case.
Hence, the total lighter area is 2 8 8 − 1 8 − 9 6 = 1 7 4 , giving the area of the shaded octagon to be 1 8 2 − 1 7 4 = 1 5 0 .