Milestone: 100,000 points! (An excuse to post a problem)

$\quad \text{Consider } G(x) = 16x^4+96x^3+224x^2+240x = 16\cdot x(x^3+6x^2+14x+15) \\ \quad G(x) = 16\cdot x(x+3)(x^2+3x+5) \\ \quad G(x) < 0 \text{ for } x \in (-3,0) \quad \color{royalblue}{\text{It must have a global minima }} \\ \quad \text{Put } G^{'}(x)=4x^3+18x^2+28x+15 = 0 \implies x = -\dfrac{3}{2} \\ \quad \text{Note that } G^{'}(x) \text{ is increasing for all } x \in \mathbb R \quad , \text{It will have only one root } \\ \quad G\left(-\dfrac32\right) = -16\cdot \dfrac{3}{2} \cdot \dfrac{3}{2} \cdot\left( \dfrac{9}{4}-3\cdot\dfrac{3}{2}+5\right) = -99 \\ \quad \text{For } G(x)+k>0 \implies k>99 \implies 40p-4p^2 > 99 \\ \quad p^2-10p+\dfrac{99}{4} < 0 \\ \quad (p-\alpha)(p-\beta) < 0 \quad \text{ Where } \alpha \text{ and } \beta \text { are the roots of the equation such that } \alpha < \beta \\ \quad \alpha<p<\beta \\ \quad \boxed{\alpha + \beta = 10}$

---

$\text{ A nice Question + A bad Title} = \text{No like }$

$f(x) = 16x^4+96x^3+224x^2+240x+40p-4p^2$

Notice that $16x^4 = (2x)^4$ . Also notice that $96x^3 = 12(8x^3) = 4(3)(2x)^3$

Recall that $(m+n)^4 = m^4+4m^3n+6m^2n^2+4mn^3+n^4$ . The two terms above fit the format of this expansion.

From this, we know that we can try to separate $(2x+3)^4$ from the function.

$(2x+3)^4 = 16x^4+96x^3+216x^2+216x+81$

$f(x)=\color{#3D99F6}{16x^4+96x^3+216x^2}+8x^2\color{#3D99F6}{+216x}+24x+40p-4p^2\color{#3D99F6}{+81}-81\\ =\color{#3D99F6}{(2x+3)^4}+8x^2+24x+40p-4p^2-81\\ =(2x+3)^4 + 8\left(x^2+3x\color{#D61F06}{+\left(\dfrac{3}{2}\right)^2-\left(\dfrac{3}{2}\right)^2}\right) + 40p-4p^2-81\\ =(2x+3)^4 + 8\left(x^2+3x+\dfrac{9}{4} - \dfrac{9}{4}\right)+40p-4p^2-81\\ =(2x+3)^4+2\left(4x^2+12x+9\right)-18+40p-4p^2-81\\ =(2x+3)^4+2(2x+3)^2+40p-4p^2-99$

Now, we know that $(2x+3)^4+2(2x+3)^2 \geq 0$ for all real $x$ . For $f(x)$ to have no real roots, we must let $f(x) > 0$ for all real $x$

$(2x+3)^4+2(2x+3)^2+40p-4p^2-99 > 0\\ \implies 40p-4p^2-99 > 0\\ 4p^2-40p+99<0\\ (2p-9)(2p-11)<0\\ \dfrac{9}{2} < p < \dfrac{11}{2}$

$a = \dfrac{9}{2},\;b=\dfrac{11}{2},\;a+b = \dfrac{9}{2}+\dfrac{11}{2} = \dfrac{20}{2} = \boxed{10}$

For significantly large $40p - 4p^2$ then by the nature of even-ordered polynomials, we must have a $f(x) > 0$ for all $x$ . Let say there has to be some range where $40p - 4p^2 > \alpha$ . Then by vieta's formula, the two boundaries are $a,b$ then $a+b = - \frac{40}{-4} = 10$ .

As there will be no real roots so I can consider four pairwise comples conjugate roots such as:

$(a+ib) ,(a-ib) ,(c+id) ,(c-id)$

products of the roots are $(a^{2} + b^{2})(c^{2} + d^{2})$

So sum of squares is always greater than zero

so $\dfrac{40p-p^{2}}{16} > 0$

which gives the inequality $p(p-10) < 0$ that is $p \in (0,10)$

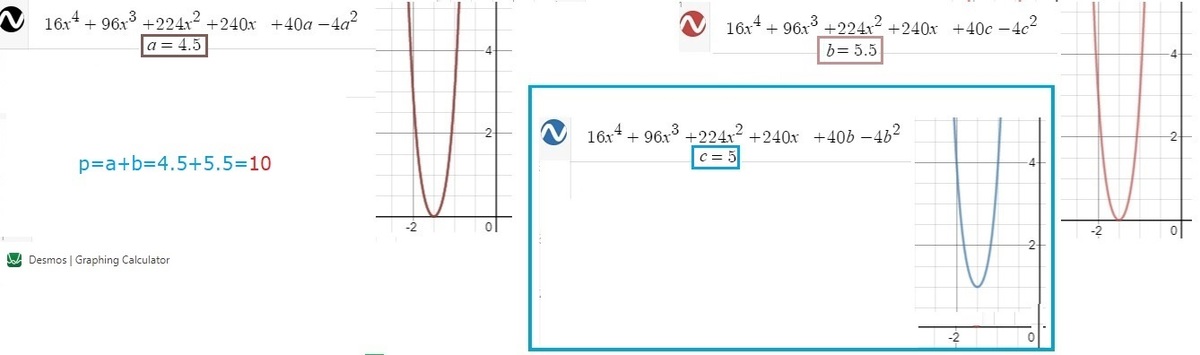
p=a+b=4.5+5,5= 10 This is just to show how the curve goes above x=0 to become not real. Graph by DESMOS.