Millions of combinations
Logic
Level
1
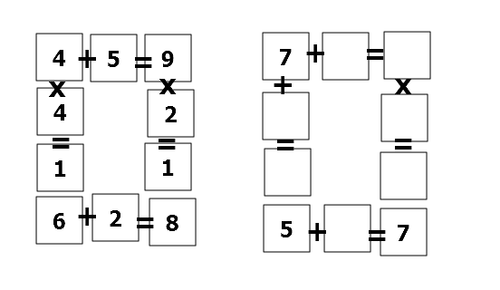The above shows two arithmetic puzzles: the left one is complete while the right one is incomplete.
Each box can only contain a non-zero digit.
Find the sum of all the missing digits in the puzzle on the right.
The answer is 27.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The bottom row reads 5 + □ = 7 , so it's clear that 2 goes in that bottom box ⇒ 5 + 2 = 7 .
The left column reads 7 + □ = some two digit number ending in 5. Notice that adding two single-digit numbers cannot give us a number larger than 18, so it must be that this column reads 7 + 8 = 1 5 .
The top row reads 7 + □ = some single digit number. This means we could be dealing with 7 + 1 = 8 or 7 + 2 = 9 across the top row. However, if we use 7 + 1 = 8 , then the right column will have 8 n = some number that ends in 7, which is not possible. Therefore, this row must read 7 + 2 = 9 .
The right column reads 9 × □ = some two digit number ending 7. The only two digit multiple of 9 that ends in 7 is 27 = 9*3, so this column must read 9 × 3 = 2 7 .
The numbers added to this puzzle were 2, 8, 1, 2, 9, 3, and 2. The sum of all these is 2 7 .