Min Max Cubics

Let $f(x) = x^3 + ax^2 + bx + c$ , and let $M = \max_{x \in [-1,1]} |f(x)|$ . Then $|f(1)| \le M$ , $|f(\frac{1}{2})| \le M$ , $|f(-\frac{1}{2})| \le M$ , and $|f(-1)| \le M$ . It follows that $|f(1)| \le M$ , $|-2f(\frac{1}{2})| \le 2M$ , $|2f(-\frac{1}{2})| \le 2M$ , and $|-f(-1)| \le M$ , which gives us the inequalities $\begin{aligned} |1 + a + b + c| &\le M, \\ \left| -\frac{1}{4} - \frac{1}{2} a - b - 2c \right| &\le 2M, \\ \left| -\frac{1}{4} + \frac{1}{2} a - b + 2c \right| &\le 2M, \\ |1 - a + b - c| &\le M. \end{aligned}$

Adding these inequalities and applying the triangle inequality, we get $\frac{3}{2} \le 6M,$ so $M \ge \frac{1}{4}$ .

For $f(x) = x^3 - \frac{3}{4} x$ , it is easy to check that $\max_{x \in [-1,1]} |f(x)| = \frac{1}{4},$ so $\min_{f \in \mathfrak{F}} \max_{x \in [-1,1]} |f(x)| = \frac{1}{4}$ .

Sorry, the answer should have been $\frac{1}{4}$ , instead of $\frac{1}{8}$ . It has been updated.

---

[Read this solution in parts, and see if you can guess the next step.]

Suppose that $F(x)$ is the monic cubic polynomial that gives us the minimum, and that the answer is $S$ . What can we likely say about $F(x)$ ?

• It makes sense that the polynomial should twist and turn about in the region $[-1, 1]$ . We most likely have 2 turning points here.
• It seems likely that $F(1) = S$ , else we can jiggle the graph slightly. Similarly, $F(-1) = - S$ .
• At the turning points, we should also have $|F(x) | = S$ , else jiggle again.

Thus, the graph "should" look like this:

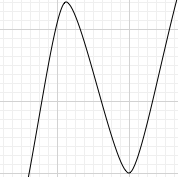
What does it remind you of? Can you guess what $F(x)$ is?

How would you continue from here? How can we show that this is indeed the optimal solution that cannot be improved?

---

[Spoiler alert]

Approach 1: From @Jake Lai :
Assuming symmetry, the graph has the form $F(x) = x (x-a) ( x + a)$ , where $a$ is to be determined such that $F(1)$ is equal to the local maximum. The maximum occurs at $x = - \sqrt{ 2a/3}$ , and thus $a = \sqrt{ 3} / 2$ . We obtain the polynomial $F(x) = x ^ 3 - 3/4 x$ .

However, the downside of this approach is that we do not get a clear path forward on how to show that this is indeed optimal. Look at Jon's solution for a way forward.

Approach 2: From Calvin Lin:
The graphs suggest that we want to look at trigonometric polynomials. We consider the Chebyshev polynomial

$T_3 (x) = \cos ( 3 arccos x ) = 4x^3 - 3x.$

From the definition, we know that the local maximum is equal to $T_3 (1) = 1$ .

Since we want a monic polynomial, let's divide by the leading coefficient to obtain $S_3 (x) = \frac{1}{4} T_3(x)$ , with the claim that the answer is equal to $\frac{1}{4} T_3 (1) = \frac{1}{4}$ .

Proof: From the definition, we know that $S_3 ( 1) = S_3 ( \cos \frac{2\pi}{3} ) = \frac{1}{4}$ and $S_3 ( -1) = S_3 ( \cos \frac{ \pi}{3} ) = - \frac{ 1}{4}$ . Suppose we have another monic cubic polynomial $M(x)$ which produces a smaller absolute max $M$ . Consider $N(x) = S(x) - M(x)$ . By definition, the degree of this polynomial is at most 2. However, we get that $N(-1) < 0, N( - \frac{1}{2} ) > 0 , N (\frac{1}{2} ) < 0, N (1) > 0$ , which indicates that this polynomial has 2 turning points and hence has degree at least 3. Contradiction.

---

Generalization.

It is now easy to generalize this to n-degree polynomials. If you go through that same diagram analysis, we realize that we want something that loops back and forth with a fixed height.

Consider $T_n(x) = \cos ( n arccos x )$ , which has leading coefficient $2^{n-1}$ . Let $S_n(x) = \frac{1}{ 2^{n-1} } T_n(x)$ . Then, the values of $S_n$ at the points $1, \cos \frac{\pi}{n}, \cos \frac{2\pi}{n} , \ldots , \cos \frac{ (n-1) \pi } { n} , - 1$ are alternatively $\frac{1}{ 2^{n-1} }$ and $- \frac{ 1}{ 2^{n-1} }$ by definition of $\cos \theta$ .

Now, suppose that there is another monic degree n polynomial $M(x)$ which produces a smaller absolute max $M$ . Considering $N(x) = S(x) - M(x)$ which has degree at most $n-1$ . However, $N(x)$ has a turning point in each of these $n$ intervals $( \cos \frac{ (k+1) \pi } { n} , \cos \frac{k\pi}{n} )$ , and thus it has degree at least $n$ , which is a contradiction.