Min value of $f(x)$

$\begin{aligned} f(x) & = (x+1)(x+2)(x+3)(x+4) & \small \color{#3D99F6} \text{Let }y = x+\frac 52 \\ & = \color{#3D99F6}\left(y - \frac 32\right) \color{#D61F06}\left(y - \frac 12\right)\left(y + \frac 12\right) \color{#3D99F6}\left(y + \frac 32\right) \\ & = \color{#3D99F6}\left(y^2 - \frac 94 \right) \color{#D61F06}\left(y^2 - \frac 14\right) \\ & = y^4 - \frac 52 y^2 + \frac 9{16} \\ & = \left(y^2 - \frac 54\right)^2 - \frac {25}{16} + \frac 9{16} \\ & = {\color{#3D99F6}\left(y^2 - \frac 54\right)^2} - 1 \end{aligned}$

Since $\color{#3D99F6}\left(y^2 - \dfrac 54\right)^2 \ge 0$ , $\implies f(x) \ge \boxed{-1}$ .

$f(x) = (x+4)(x+1)(x+2)(x+3) = (x^2+5x+1)(x^2+5x+6) =(x^2+5x+5-1)(x^2+5x+5+1) = (x^2+5x+5)^2-1$ . As $x^2+5x+5 = 0$ has real solutions ( $\Delta=\sqrt{b^2-4ac} = \sqrt{25-20}>0$ ), The minimum value of $f(x)$ is $-1$ .

I would like to preface this proof by saying I am really impressed with myself for coming up with this shortcut on the spot and have no idea how I did it so fast.

Now, we could use the generic maxima and minima technique by seeing where the derivative equals zero, however if we do that now we are going to end up with a cubic equation which will not be straightforward to solve. So instead, I'm going to create a new function $g(x)$ where: $g(x)=f\left(x-\frac{5}{2}\right)$ This new function will have the same maximum and minimum values as $f(x)$ , as it simply moves the graph of $y=f(x)$ by $\frac{5}{2}$ units to the right: 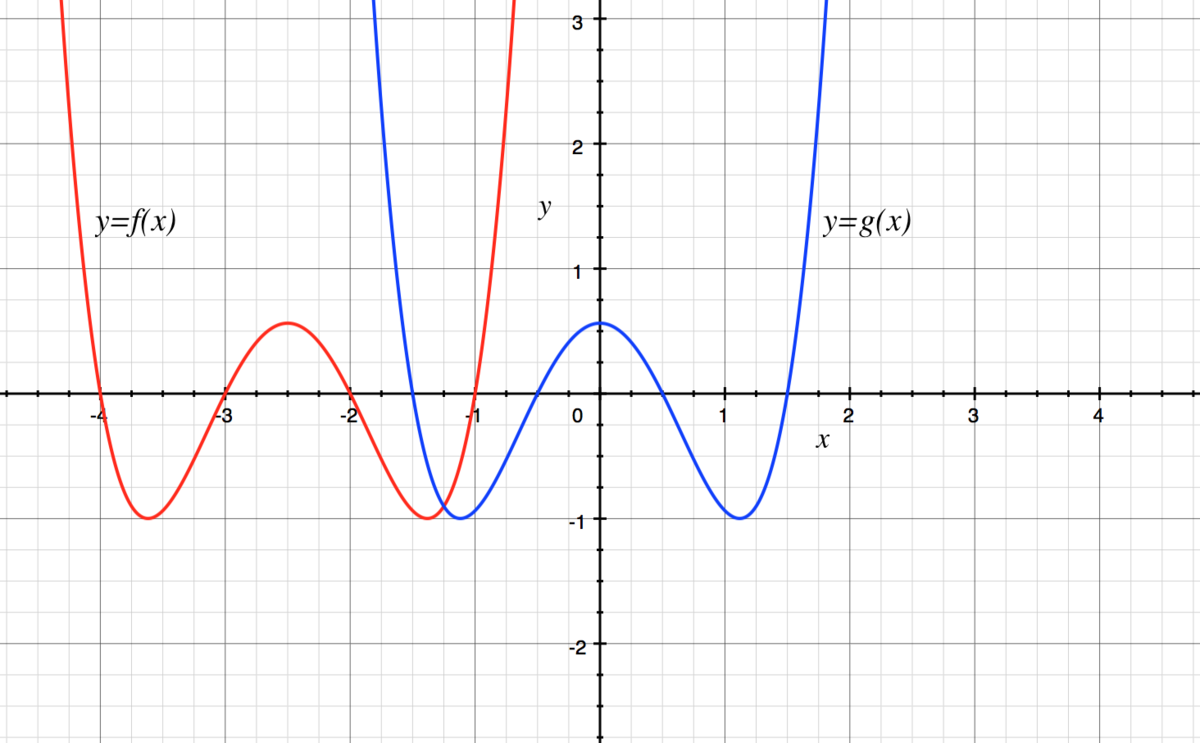The advantage of this will be clear in a moment. $\begin{aligned}g(x)&=\left(x-\frac{5}{2}+3\right)\left(x-\frac{5}{2}+2\right)\left(x-\frac{5}{2}+4\right)\left(x-\frac{5}{2}+1\right)\\ &=\left(x+\frac{1}{2}\right)\left(x-\frac{1}{2}\right)\left(x+\frac{3}{2}\right)\left(x-\frac{3}{2}\right)\\ &=\left(x^2-\frac{1}{4}\right)\left(x^2-\frac{9}{4}\right)\end{aligned}$ Now you can see from both the graph, and the fact that there are now only $x^2$ terms, that this new function is even , meaning the resulting derivative will be simpler to work with. $\begin{aligned}g(x)&=\frac{1}{4^2}\left(4x^2-1\right)\left(4x^2-9\right)\\ &=\frac{1}{16}\left(16x^4-40x^2+9\right)\\ g'(x)&=\frac{1}{16}\left(64x^3-80x\right)\\ &=4x^3-5x\end{aligned}$ Continuing with the maxima and minima method, we let the derivative equal zero to find the maximum and minimum turning points in the curve. This cubic derivative is now really easy to solve thanks to the zero factor: $4x^3-5x=0\\ 4x\left(x^2-\frac{5}{4}\right)=0\\ x\left(x+\frac{\sqrt5}{2}\right)\left(x-\frac{\sqrt5}{2}\right)=0\\ x=0,\frac{\sqrt5}{2},-\frac{\sqrt5}{2}$ Now we can substitute these values back into $g(x)$ to get the local maximum and minimum $y$ values. Note that since $g(x)$ is even, $g\left(\frac{\sqrt5}{2}\right)$ and $g\left(-\frac{\sqrt5}{2}\right)$ will yield the same result, so we only have to text $g(0)$ and $g\left(\frac{\sqrt5}{2}\right)$ . $\begin{aligned}g(0)&=\left(\left(0\right)^2-\frac{1}{4}\right)\left(\left(0\right)^2-\frac{9}{4}\right)&&&g\left(\frac{\sqrt5}{2}\right)&=\left(\left(\frac{\sqrt5}{2}\right)^2-\frac{1}{4}\right)\left(\left(\frac{\sqrt5}{2}\right)^2-\frac{9}{4}\right)\\ &=\left(-\frac{1}{4}\right)\left(-\frac{9}{4}\right)&&&&=\left(\frac{5}{4}-\frac{1}{4}\right)\left(\frac{5}{4}-\frac{9}{4}\right)\\ &=\frac{9}{16}&&&&=\left(1\right)\left(-1\right)\\ &&&&&=-1\end{aligned}$ In a full proof we would have to show whether these are maximum or minimum values and whether they are local or global. However, since the curve is quartic and continuous and the leading coefficient is positive, we can conclude that the smaller value of $-1$ is the global minimum of $g(x)$ .

Since $g(x)$ and $f(x)$ are the same function except translated along the x-axis, they have the same global minimum, and so the final answer is $\boxed{-1}$

let z=x^2+5x, f(x) =(z+4)(z+6) = (z+5)^2 – 1 , min of f(x) = -1