MindMine #2
In the grid below, the number in each cell represents the number of neighboring cells which contain a mine (including diagonals but not including the cell itself). How many of the cells contain mines?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.

In this solution, grey squares will show the actual shading of the cells, and all other colours are for easy reference. A black cross through a cell will mean it definitely isn't shaded. I have tried to make this as easy as possible to understand so reading slowly, it should be clear enough.
In the picture above, look at the red square. It needs one shaded square around it. If it was the yellow square that was shaded, then neither of the greens would be shaded. This would then mean that the yellow square would need 4 surrounding it. We've already said that the greens aren't shaded, which would leads to only 3 possible squares (orange and red). Therefore, this is impossible, and the yellow square is not shaded. Now we know that exactly one of the green squares is shaded. To satisfy the requirements of the yellow square, this means that the red and both orange squares are shaded (along with one of the greens).
In the picture above, look at the blue square. It already has two shaded neighbours, meaning that the purple square is not shaded.
In the picture above, look at the red square. It needs to have 3 shaded neighbours. Since it already has 1, and the orange squares are the only remaining neighbours, the orange squares are shaded. Now that both oranges are shaded, the yellow square is fully satisfied, meaning that the green square isn't shaded.
In the picture above, look at the blue square. It already has 3 shaded neighbours, meaning that neither of the red cells are shaded. The purple square now needs one more shaded neighbour. Since neither of the red are shaded, the orange is the only remaining possibility so the orange square is shaded.
In the picture above, look at the red square. It already has its 3 shaded neighbours, meaning that the orange square isn't shaded. Now that the orange square isn't shaded, the only remaining square which could fill the requirements of the yellow square is the green one, so the green square is shaded.
In the picture above, look at the blue square. It is already satisfied, meaning that the purple square isn't shaded. As the purple isn't shaded, the red square still needs an extra shaded neighbour. The only remaining possibility is the orange, so the orange square is shaded. Finally, the yellow square is fully satisfied already, so the green square isn't shaded.
This leaves us with a final diagram looking like this: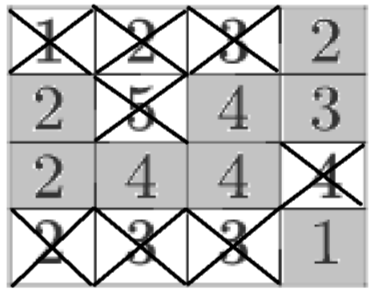
From here, we can clearly see that 8 squares are shaded.