MindMine #6

Logic Level 3

In the grid below, the number in each cell represents the number of neighboring cells which are shaded, including the diagonals but not including the cell itself: $\large{\begin{array}{|c|c|c|c|} \hline 1 & 4 & 3 & 2 \\\hline 2 & 3 & 3 & 3 \\\hline 2 & 4 & 5 & 3 \\\hline 1 & 1 & 2 & 1 \\\hline \end{array}}$ How many of the cells are shaded?

8 6 7 5

2 solutions

Stephen Mellor
Jun 5, 2018

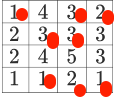
Consider the blue cells. They mean that exactly one of the orange cells is shaded, and both the green cells are shaded, and that the blue 4 cannot be shaded.

The blue cell now means that the orange cell isn't shaded. From the three on the top row, we then know that the blue and green cells are both shaded.

The blue cells now mean that none of the orange cells are shaded.

The blue cells now mean that the orange cells are shaded.

The blue cell now means that the orange cells aren't shaded.

The blue cell now means that the orange cell must be shaded. However, the orange cell already has one shaded neighbour, so the blue cell isn't shaded.

This leaves us with the following diagram, from which we can see that $\boxed{8}$ cells are shaded.

Siva Budaraju
Jun 5, 2018

Red mark means that the cell is shaded.

MindMine #6

2 solutions

0 pending reports