Minimario's diagonal
Let A B C D be a square with side length 2 and let X be a point outside the square such that X A = X B = 2 . The length of the longest diagonal in pentagon A X B C D can be expressed as x . What is the value of x ?
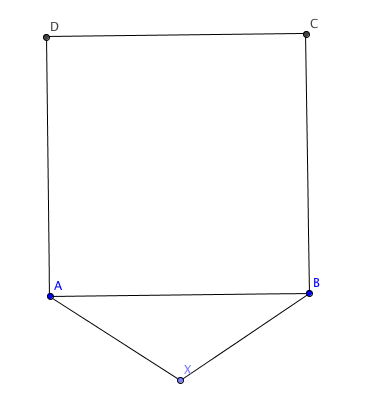
This problem is posed by Minimario M.
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
18 solutions
Moderator note:
Good approach. We need to calculate the various lengths, in order to conclude what the maximum length is. This is a common oversight made by many solutions below.
Note that if A B C D is not a square, it need not be true that X C > C B . Think of a very skinny rectangle.
THE BEST METHOD TO SOLVE IT
The longest diagonal of pentagon A X B C D is the line D X and C X (Check this out about diagonal ), where they have same length. Then, we denote the length of them as k . Finding k , we get the new triagle A X D or B X C , in here, I assume that, I choose the triagle B X C , actually both of A X D and B X C same.
Then, look the triangle B X C , you get the side, B C = 2 , B X = 2 , and C X is the longest diagonal which we have to find it as k . Get the x using Law of Cosines . But, We have to know the angle of C B X to get k . We know that is 1 3 5 ∘ . How? We know that from ∠ A B C + ∠ A B X = 9 0 ∘ + 4 5 ∘ . Finally, using Law of Cosines :
c o s 1 3 5 ∘ = 2 . B X . B C B X 2 + B C 2 − k 2
You must get the k as well as C X , the longest diagonal of the pentagon is 1 0 , so x = 1 0 .
Using pythagoren formula is more simple while i like to see your solution
we use the same solution :)
Let the mid point of AB is M. Then AM=M=1. Mid point of CD is N.Then CN =ND=1; so MN=2 & XM=1.hence the longest diagonal is XC or XD of length= XN^2+NC^2=10^1/2 . so,x=10.
AM=MB=1
very good method, didn't think of it before..
Center Cartesian coordinates at A. Then D is at (0,2) and X is at (1,-1) since AXB is isosceles. Thus, DA has length 3 2 + 1 2 = 1 0 .
Woah i posted my solution and then saw yours, which is almost the same.
The longest diagonal are DX and CX.
DX or CX= √(3²+1²)
=√10
the longest diagonal can be express as √x, therefore x=10
longest diagonal= line CX and line DX I'll choose line DX D X 2 = D A 2 + A X 2 − 2 ( D A ) ( A X ) c o s ( D A X ) D A = 2 and A X = 2 let O=midpoint between A and B A O = 2 A B = 2 2 = 1 O X 2 = A X 2 − A O 2 = ( 2 ) 2 − 1 2 = 2 − 1 − 1 so O X = 1 O A X = a r c t a n A O O X = a r c t a n ( 1 1 ) = 4 5 degree D A X = 9 0 + O A X = 9 0 + 4 5 = 1 3 5 degree c o s D A X = c o s 1 3 5 = − 2 1 D X 2 = D A 2 + A X 2 − 2 ( D A ) ( A X ) c o s ( D A X ) = 2 2 + ( 2 ) 2 − 4 2 2 − 1 D X 2 = 4 + 2 + 4 = 1 0 so the answer is 1 0
- DX is the longest diagonal in pentagon AXBCD.
- We have AX= BX= √2 and AB=2, so ABX is the right-angled and isosceles triangle at X.
- Let E be the midpoint of AB and F be the midpoint of CD. => XF^2 = AX^2-AF^2 => XF=1.
- And EF is parallel with AD and BC, so AD=EF=2.
- We have EX=FX+EF=1+2=3.
- E is the midpoint of DC, so DE=DC/2=1.
- According to Pythagoras theory, we have DX^2 = XE^2 + DE^2 = 3^2 +1^2 = 10. => DX = √10
To begin with, let us notice a few things about the triangle A B X . We know that the height h of it drawn towards its side A B (intersecting into a point N ) divides A B into 2 equal parts, each having a value of 1 . Now, we are aware that B X = A X = 2 . Thus, we can easily find the height of A B X by using the Pythagorean Theorem, resulting in h = 1 . This shows us that the triangles A N X and B N X are both isosceles, as well as right triangles. Therefore, it is obvious that both angles A B X and B A X equal 4 5 ∘ .
Now let us turn our attention to the diagonals of the square A B C D . We can see that A C = B D = 2 2 . We also know that the angles B A C and A B D both equal 4 5 ∘ as well, since the diagonals of a square split its angles exactly in half.
From all this we may also notice that the angles X A C and X B C are 9 0 ∘ ( 4 5 ∘ + 4 5 ∘ ) .
The diagonals we are actually looking for are X D and X C , which both happen to be the hypotenuses of the right triangles X A C and X B D . Now, by using the Pythagorean Theorem once more we can easily find that X D = X C = 1 0 .
Since we know that x = 1 0 we can easily find that x = 1 0 , which is the correct answer to the problem.
The triangle ABC is rectangular. So  = 135°. By law off cosines: DX² = DA² + AX² - 2DA AX cos135 So, x = DX² = 10.
use a xy coordinate system taking origin at X. now find the coordinate of point D that is (-1,3). now from distance formula find the length of line XD. XD = [ (3-0)^2 + (-1-0)^2 ]^0.5 = (10)^0.5 = (x)^0.5 this implies x=10.
Obviously, the answer is the length of XD First let's calculate the perpendicular distance from X to AB: let F be a AB midpoint (XF = 1) since XA = XB therefore XF is perpendicualr on AB XF^2 = XA^2 - AF^2 = 2 - 1 XF = 1
Now we need to calculate XD: perpendicular distance from X to DC (V)= AF + AD = 1+2 = 3 perpendicular distance from X to AD (H)= AF = 1 XD^2 = V^2 + H^2 XD^2 = 10 XD equal square root 10
By assigning x and y coordinates to point D, A, and X, the distance formula can find X^(1/2). D can be the origin, (0,0), and since side DA is length 2, then A can be (0,-2). An altitude drawn from side AB is drawn from the midpoint of AB, which is length 2 again, so the x coordinate of X is 1. By Pythagorean's theorem, 1^2+1^2=c^2, and c=2^(1/2), so the y coordinate of X is A's -2-1, or -3. Then, by the distance formula, ((0-1)^2+(0-3)^2)^(1/2)=(1+9)^1/2=(10)^1/2. X is then 10.
By Pythagoras you get the diagonal of the square is sqrt(8)=2sqrt(2) which is double XA. By drawing a second square right below the one drawn, and by drawing the diagonal you are asked for (DX) a rectangle square is formed with sides 3 and 1.
Draw a line DX
DAB = 90 degree
Draw a line perpendicular to AB from X and label Z
XZ = 1
Since ABX is isosceles triangle , so , XAZ is 45 degree
@ = angle DAX
Use cosine formula as
c^2 = a^2 + b^2 - 2ab cos @
c^2 = (2)^2 + (sqrt 2)^2 - 2(2) (sqrt 2) cos @ = 10
it is easily see that XC or XD is the longest diagonal of the pentagon
from the side of XA, XB and AB, we found that XAB is a right-angled triangle
ie. <AXB=90 (
(
2
∗
2
^2)\=2)
then we get <XBC=135
by using cosine rule, let XC=√x
x=2^2 +(\sqrt2) ^2 -2(2)(√2)cos 135
x=10
Moderator note:
Why must X C / X D be the longest diagonal? How do you know immediately that X C > C B ?
For this one, you will need to think outside the box, er, triangle. Using the information given, it is possible to determine that Triangle AXB is a 45-45-90 when split in half (we'll call that point y). The length of segment YB is 1 and so must be segment XY. We then add the length of CB and XY (making a segment down the pentagon with a length of 3). Finally we make a diagonal line from X to C. From there, all you do is use the Pythagorean Theorem to find the length of XC.
Let E be the midpoint AB. Triangle AEX is a right triangle with lengths 1, s q r t ( 2 ) , and EX. Solving for EX (using Pythagorean theorem or special triangles) gives us a length of 1
The longest diagonal is DX ( or CX) because it is longer than the diagonal of a square.
Let F be the midpoint of DC. We form a right triangle DFX with lengths DF=1, FX=FE+EX=2+1=3, and DX.
Solving for DX (using Pythagorean theorem) gives us s q r t ( 1 0 ) , thus x=10
It is clear that our longest diagonal is D X = C X = 1 2 + 3 2 = 1 0 . ■
As we see on the picture, there are two diagonals A C = B D and C X = D X . Let find the length of diagonal A C and C X by using Pythagorean Theorem
A C 2 = A B 2 + B C 2 = 2 2 + 2 2 = 8
∴ A C = 8
Let B ′ be a point so A B ′ and B ′ X is perpendicular, then we found that B B ′ = B ′ X = 1 .
C X 2 = ( A B + B B ′ ) 2 + B ′ X 2 = ( 2 + 1 ) 2 + 1 2 = 1 0
∴ C X = 1 0
Since A C < C X , then the longest diagonal is C X = 1 0 imply x = 1 0 .