Minimize the Perimeter
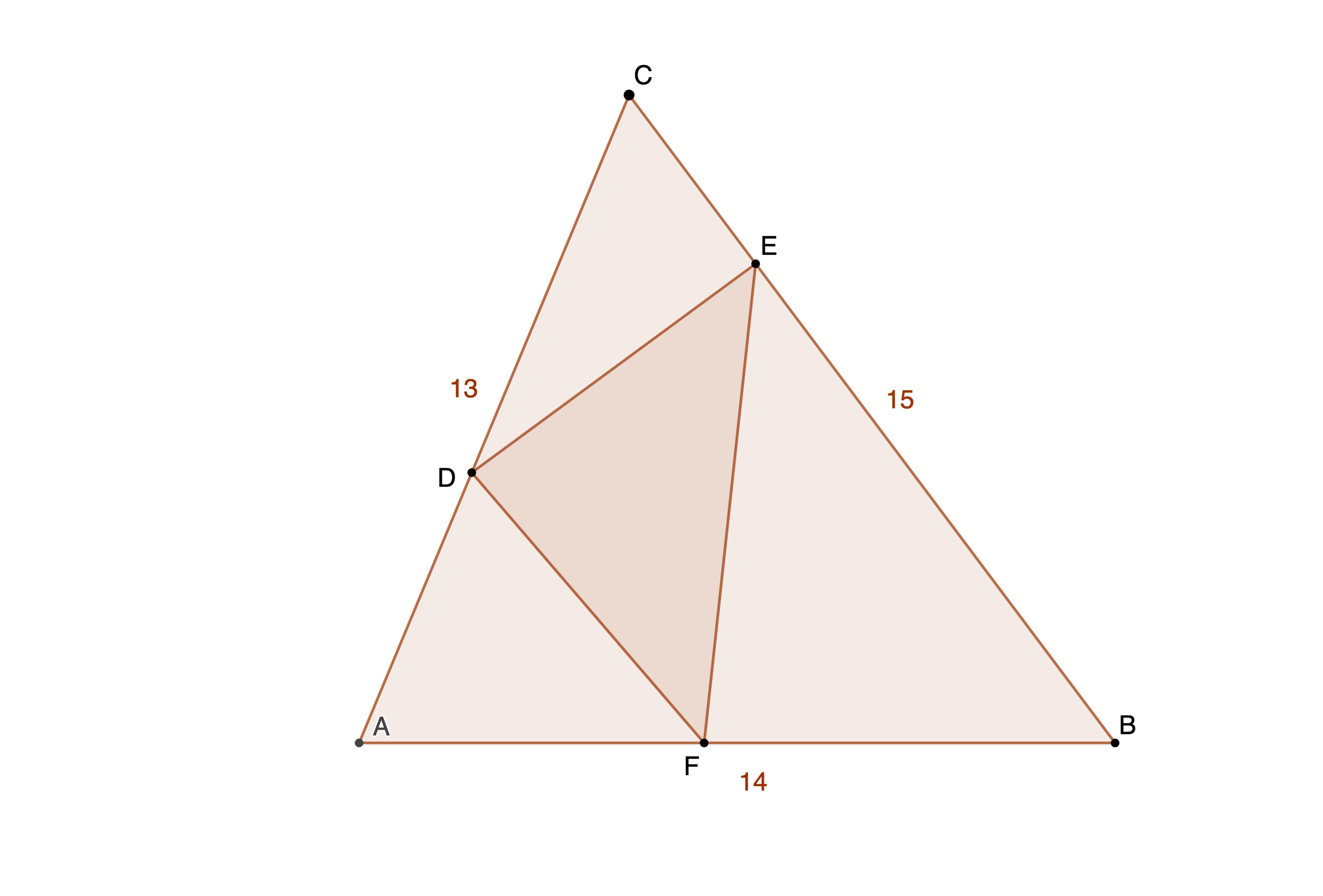
is a 13-14-15 triangle. is constructed by placing one vertex on each side of . Find the smallest possible perimeter of . If this perimeter is expressed as , where and are coprime integers, submit .
The answer is 1409.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Reflect △ A B C in C B and then reflect △ A ′ B C in C A ′ .
Then the perimeter of △ D E F is equivalent to F E + E D ′ + D ′ F ′ ′ , which is at a minimum when E and D ′ are on F F ′ ′ .
Since reflections preserve lengths and angles, △ A B C ≅ △ A ′ B C ≅ △ A ′ B ′ C , so C F = C F ′ ′ and ∠ F C F ′ ′ = 2 ∠ A C B .
By the law of cosines on △ F C F ′ ′ , F F ′ ′ = C F 2 + C F 2 − 2 ⋅ C F ⋅ C F cos 2 ∠ A C B = 2 ⋅ C F ⋅ sin A C B .
Since 2 ⋅ sin A C B is a positive constant, F F ′ ′ reaches a minimum when C F is a minimum, which is when C F is the altitude of △ A B C . Therefore, the minimum perimeter is P min = 2 h c sin C , where h c is the altitude of △ A B C from C .
Substituting in area of triangle equations T = 2 1 h c c and T = 2 1 a b sin C , we get P min = a b c 8 T 2 .
By Heron's Theorem, the area of △ A B C is T = 8 4 . Therefore, P min = a b c 8 T 2 = 1 3 ⋅ 1 4 ⋅ 1 5 8 ⋅ 8 4 2 = 6 5 1 3 4 4 , so p = 1 3 4 4 , q = 6 5 , and p + q = 1 4 0 9 .